Пусть О - точка пересечения медиан.
Если взглянуть на хорошо нарисованный чертеж (то есть такой, где медианы треугольника взаимно перпендикулярны), можно увидеть три прямоугольных треугольника (их там больше, но нам только эти нужны) АОВ, АОЕ и BOD.
если обозначить КОРОТКИЕ ОТРЕЗКИ медиан, как y и z (ОD = z, при этом по свойству медиан ОА = 2*z, и так же OE = y, поэтому ОВ = 2*y), а неизвестную сторону АВ = х, то из этих треугольников сразу получается 3 равенства:
(2*y)^2 + (2*z)^2 = x^2; то есть х^2 = 4*(y^2 + z^2);
z^2 + (2*y)^2 = BD^2 = 4;
(2*z)^2 + y^2 = AE^2 = (3/2)^2 = 9/4;
Два последних уравнения можно честно решить, найти y и z, и вычислить х. Но раз нам надо только найти сумму квадратов y и z, можно сложить эти 2 последних уравнения, и мы сразу получим ответ.
5*(y^2 + z^2) = 4 + 9/4 = 25/4; (y^2 + z^2) = 5/4; x^2 = 5;
ответ: АВ = корень(5)
Диагональ делит угол пополам - эта диагональ - биссектриса.
Биссектриса трапеции отсекает от нее равнобедренный треугольник. В самом деле:
В треугольнике ВСД угол СВД=углу ВДА как накрестлежащие, угол ВДС=углу ВДА как половины угла АДС. Следовательно, угол ВДС=углу СВД.
ВС=СД.
В трапеции треугольники, образованные диагоналями и основаниями, - подобны. Они имеют по равному вертикальному углу при пересечении биссектрис и равные накрестлежащие углы.
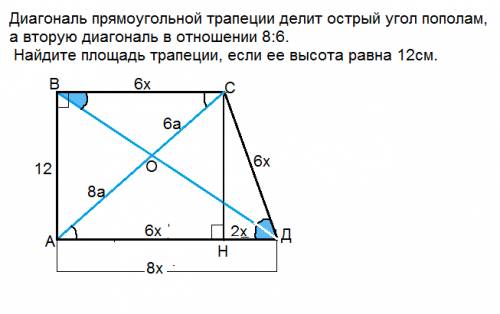
k=AО:ОС=8:6
АД:ВС=8:6
Пусть коэффициент этого отношения равен х
Тогда АД=8х, ВС=6х
Опустим из С высоту СН=12.
АН=ВС, НД=8х-6х=2х, СД=ВС=6х
По т.Пифагора
СД²-НД²=СН²
36х²-4х²=144
32х²=144
х=√4,5=1,5√2 ⇒
ВС=9√2
АД=12√2
S (АВСД)=(21√2)*12:2=126√2 см²
Средняя линия =x
Большее основание =4+х
Тогда :
Х=0,5(х+8)
Х=0,5х+4
0,5х=4
Х=8(средняя линия трапеции)
ответ : средняя линия трапеции =8см