Внешним углом треугольника называется угол смежный с каким-либо углом этого треугольника.
Смотри приложение :
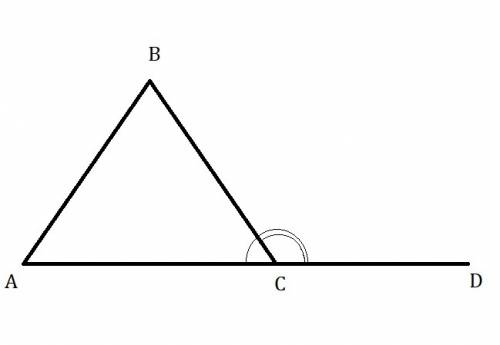
Дан ΔАВС .
При вершине С начертим внешний угол , обозначим его ∠ВСD.
Теорема : Внешний угол треугольника равен сумме двух углов не смежных с ним.
Дано : ΔАВС
Внутренние углы треугольника: ∠ВАС , ∠АВС , ∠ВСА
Внешний угол при вершине С: ∠ВСD
Доказать : ∠ВСD = ∠ВАС + ∠АВС
Доказательство.
1) По теореме о сумме углов треугольника :
Сумма углов (внутренних) треугольника равна 180 градусов.
∠ВАС + ∠АВС + ∠ВСА = 180°
∠ВАС + ∠АВС = 180° - ∠ ВСА
2) По свойству смежных углов:
Сумма смежных углов равна 180 градусов.
∠ВСD + ∠ BCA = 180°
∠ВСD = 180° - ∠BCA
3) ∠ВСD = ∠BAC + ∠АВС = 180° - ∠ВСА
∠ВСD = ∠BAC + ∠ABC , что и требовалось доказать...
Прямая а делит плоскость на 2 части. Скажем, верхнюю и нижнюю (правую и левую и т.п.). Точка Х принадлежит одной полуплоскости (любой), тогда концы отрезков M и D, в случае их пересечения прямой а, будут лежать в другой полуплоскости. Если обе точки отрезка лежат в одной полуплоскости, ограниченной прямой, то эту прямую такой отрезок не пересекает.
Если пересечением отрезков [XM] и [XD] с прямой а являются концы этих отрезков M и D (нижний рисунок), то речь о пересечении отрезком [MD] прямой а также не идет, поскольку отрезок [MD] является частью прямой а и имеет с ней более одной общей точки. А при пересечении отрезком прямой точка может быть только одна.