118°, 118°, 62°, 62°
Объяснение:
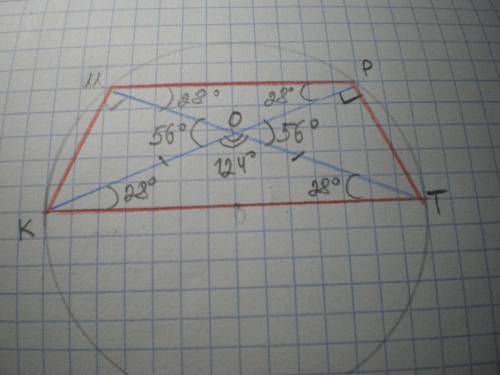
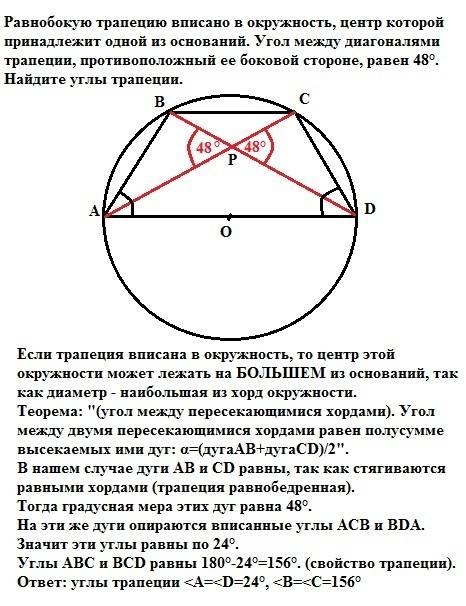
Дано: КМРТ - трапеция, МК=РТ, КТ=D (окружности), КР и МТ - диагонали, ∠РОТ=∠МОК=56°. Найти ∠К, ∠М, ∠Р, ∠Т.
Решение: ΔКМТ=ΔТРК, т.к. КР=МТ как диагонали равнобедренной трапеции, КМ = РТ по условию, сторона КТ - общая. Значит, ∠ОКТ=∠КТО.
∠КОТ=180-56=124°; ∠ОКТ=∠КТО=(180-124):2=28°.
ΔМОР; ∠МРО=∠ОМР=∠ОКТ=∠КТО=28° как внутренние накрест лежащие при МР║КТ и секущих МТ и КР.
∠КМТ=∠КРТ=90° как углы, опирающиеся на диаметр окружности.
∠М=∠Р=90+28=118°
∠К=∠Т=180-118=62° по свойству углов трапеции, прилежащих к боковой стороне
олучившаяся фигура имеет сложную поверхность.
Это цилиндр, к основанию которого прикреплен конус, а с другой стороны точно такой же конус вырезан.
Площадь этого тела вращения равна площади боковой поверхности:
цилиндра ВСС₁ В₁ плюс
2 площади боковой поверхности конусов ВАВ₁ и СДС₁
Радиусом является высота ромба, высотой цилиндра и образующей конусов является сторона ромба.
Формулы:
Площадь боковой поверхности:
цилиндра Sбок=2πRH=2πRH
конуса Sбок=πRL
S искомое =2πha + πha =3 πha
Высоту и сторону необходимо найти.
Для начала найдем вторую диагональ:
S=D·d:2
600=30·D:2
1200=30·D
D=1200:30=40 дм
Сторону найдем по теореме Пифагора из прямоугольного треугольника с катетами - половина каждой диагонали и гипотенузой - сторона ромба а
а²=15²+20²
а²=625
а=25
Высоту найдем из половины площади ромба 300 дм².
S=ah
300=25h
h=300:25= 12 дм
R=h
H=L=a
S искомое =2πha + πha =3 πha
S тела вращения = 3 π 12·25 = 900 πдм