корень из 169 = 13 см
расстояние равно от вершины до основания 13см
2) угол dod1 = 45 градусов, . в треугльника dod1 угол d = 90 градусов, => треугольник dod1 = прямоугольный => угол dod1 = углу od1d => od = dd1 = h. od = 1/2 * db = 1/2* корень из( 144 + 256) = 1/2 * 20 = 10. найдем площадь сечения через формулу 1/2 * od1 * ac. ac = 20, od1 = корень из(100+100) = 10√2 => s acd1 = 1/2 * 20 * 10√2 = 100√
3) проекцию катета отметим как х
проекцию гипотинузы как y
решаем:
х=10*cos60град.=5 дм.
ад=√(100-25)=√75
ав=√(100+100)=√200
y=√(200-75)=√125=15 дм.
ответ:
проекция катета равна 5дм;
проекция гипотенузы равна 15дм.
Рассмотрим все случаи неравенства треугольника. Всего 2 случая, НО только один из них верный. Докажем это.
Во-первых, вспомним, что сумма двух сторон треугольника должна быть больше третьей стороны.
Проверим это:
Возьмём случай, где основание нашего равнобедренного треугольника равно 72 см, а боковые стороны по 36 см, ибо они по правилу равны. Проверим, существует ли такой треугольник, следуя теореме (выделена выше наклонным курсивом).
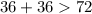 - это неверно;
- это неверно;
 - это верно;
- это верно;
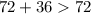 - это верно.
- это верно.
Поскольку первый случай неверный, то такого треугольника не существует.
То есть боковые стороны нашего треугольника равны по 72 см.
(рисунок к задаче прикреплён ниже)
ответ: 5).→ Задача №6.Гипотенуза - самая большая сторона в прямоугольном треугольнике, поэтому она не может равняться в данной задаче 11 см, поскольку это не самая большая цифра здесь. Получается подходит вариант 5) 11 см, т.к. гипотенуза всегда больше катета.
ответ: 5).
Биссектриса делит угол пополам, значит одна сторона x, другая 2х
все эти углы в сумме равны 180
теперь можно составить уравнение
х+2х+60=180
3х=120
х=40
2*х=80
ответ: 40, 80