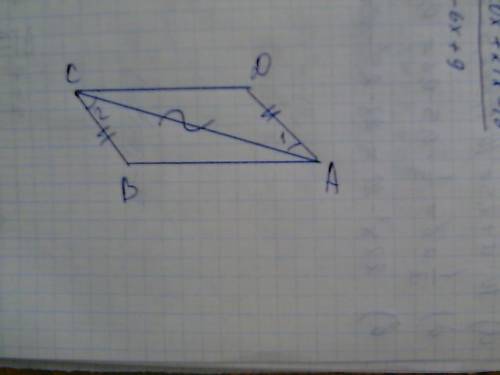
Как известно, диагонали точкой пересечения делятся пополам, а противоаоложные стороны пар-мма равны. Следовательно, противоположные по отношению друг к другу треугольники равны(по 3-ему признаку равенства треугольников), и площади их тоже равны.
Осталось доказать, что площади двух "смежных" треугольников равны. Рассмотрим их. Одна сторона у них общая, примем за основание сторону, лежащую на диагонали. Эти стороны у треугольников равны, т.к. точкой пересечения, повторюсь, диагонали делятся пополам. Прощадь треугольника у нас равна половине основания, умноженного на высоту, проведенную к основанию. Проведи к основаниям треугольников высоту - это будет один и тот же отрезок.
Мы получили - основания у треугольников равны, высоты равны.
Теорема доказана.
Пусть один угол - X, тогда второй - 180-Х.
Биссекриса делит угол пополам, т.е. первый угол будет разделен на два одинаковых угла, равных Х/2, второй - на 2 одинаковых угла, равных 90-x/2.
Тогда угол между биссектрисами будет 180-Х/2-90+Х/2 = 90 гр. То есть, биссектрисы смежных углов взаимно перпендикулярны.