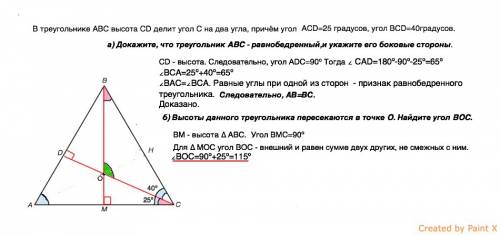
В треугольнике ABC высота CD делит угол C на два угла, причём угол ACD=25 градусов,угол BCD= 40 градусов.
а) Докажите, что треугольник ABC - равнобедренный,и укажите его боковые стороны.
СD - высота. Следовательно, угол АDС=90º
Тогда ∠ САD=180º-90º-25º=65º
∠ВСА=25º+40º=65º
∠ВАС=∠ВСА. Равные углы при стороне АС - признак равнобедренного треугольника. ⇒ АВ=ВС
Доказано.
б)
Высоты данного треугольника пересекаются в точке O. Найдите угол BOC.
ВМ - высота ∆ АВС. Угол ВМС=90º
Для ∆ МОС угол ВОС - внешний и равен сумме двух других, не смежных с ним.
∠ВОС=90º+25º=115º
а)
По условию все стороны треугольника равны а, а все углы равностороннего треугольника равны 60 градусов:
б)
Чтобы определить угол между векторами АС и СВ нужно совместить их начала, например, перенести параллельным переносом вектор АС так, чтобы точка А совместилась с точкой С. Тогда будет видно, что углом между этими векторами будет угол, смежный с углом АСВ, равный 180-60=120 градусов:
в)
Так как BD высота к АС, то векторы ВD и АС перпендикулярны, скалярное произведение перпендикулярных векторов равно 0:
г)
Произведение вектора само на себя (скалярный квадрат) равно квадрату его модуля, угол в данном случаем между одним и тем же вектором равен нулю: