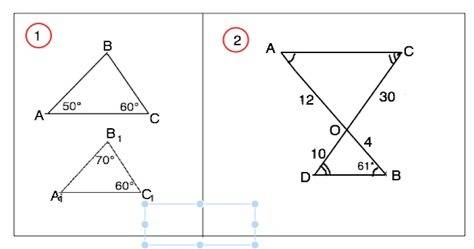
1) Сумма углов треугольника 180°. В ∆ АВС угол В=180°-50°-60°=70°. В ∆ А1В1С1 угол А1=180°-708-608=50°. Треугольники АВС и А1В1С1 подобны по равенству всех углов.
2) По условию АС║BD, АВ и СD - секущие. Образовавшиеся при пересечении секущими параллельных прямых накрестлежащие углы равны. ⇒ ∠СAО=∠DBO=61°. Треугольники АОС и BOD подобны по равенству накрестлежащих углов, а стороны, содержащие вертикальные углы при О - пропорциональны. k=АО:ВО=12:4=3, k=СО:DO=30:10=3. Отношение площадей подобных фигур равно квадрату коэффициента их подобия. S(AOC):S(BOD)=k²=3²=9
Угол В=105º,
угол С=45º
Найдем третий угол треугольника: угол А=180-*105+45)=30º
Угол А - наименьший, и против него лежит наименьшая сторона ВС ∆ АВС.
Проведем высоту ВН и получим равнобедренный прямоугольный треугольник ВНС.
ВН=НС
По т. Пифагора ВН=7
Или ВН=ВС*sin 45º=7
Катет ВН прямоугольного ∆ ВАН противолежит углу 30º и равен половине гипотенузы ВА
АВ Найдем угол А - равен 30º
Этому углу противолежит сторона ВС =7√2
Тогда по т.синусов
АВ:sin 45º=BC:sin 30º
(АВ√2):2=(7√2):0,5⇒
АВ=7*2=14 см