Решение
sin (pi/2+t)-cos(pi-t)+tg(pi-t)+ctg(5pi/2-t) = cost + cost - tgt + tgt =2cost
Объяснение:
sin (π/2 + t) - cos (π - t) + tg (π - t) + ctg (5π/2 - t). Для упрощения данного выражения используем формулы приведения. По формулам приведения: sin (π/2 + t) = cos t; cos (π - t) = – cos t; tg (π - t) = – tg t; ctg (5π/2 - t) = tg t. Таким образом, мы пришли к выражению: cos t - (– cos t) + (– tg t) + tg t = (раскроем скобки, если перед скобками стоит знак минус "-", то знак слагаемого в скобках необходимо поменять на противоположный) = cos t + cos t - tg t + tg t = (- tg t и tg t взаимно уничтожаются) = 2cos t. ответ: sin (π/2 + t) - cos (π - t) + tg (π - t) + ctg (5π/2 - t) = 2cos t.
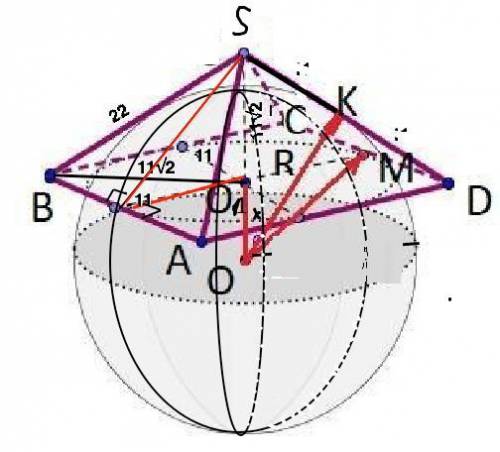
Радиус r окружности, вписанной в основание пирамиды, равен половине стороны квадрата.
O1M = r = 22/2 = 11.
Центр сферы находится на прямой, проходящей через высоту пирамиды (это для правильной пирамиды).
Составит систему уравнений из треугольников, включающих R к стороне основания, и к боковому ребру.
Это соответственно треугольники OKS и OMS.
Обозначим отрезок О1О = х.
Для пирамиды с равными рёбрами угол наклона бокового ребра к основанию равен 45 градусов. Отсюда вывод: треугольник OKS – прямоугольный равнобедренный.
KS = kO = R = (ОО1 + Н)/√2 = (х + Н)/√2.
Высота Н = L*sin 45° = 22*(√2/2) = 11√2.
Тогда R = (х + 11√2)/√2. (1)
Из прямоугольного треугольника МОО1 получаем R² = 11² + x². (2)
Возведём уравнение (1) в квадрат.
{R² = ((ОО1 + Н)/ √2)² = ((х + 11√2)/ √2)² = (х² + 22√2*х + 242)/2. (3)
Приравняем правые части уравнений (2) и (3).
(х² + 22√2*х + 242)/2 = 121 + х²,
х² + 22√2*х + 242 = 242 + 2х2.
Приведя подобные, получаем х² - 22√2*х = 0 или х(х - 22√2) = 0.
Имеем 2 корня: х = 0 и х = 22√2.
Второе значение даёт точку касания боковых рёбер на длине, равной радиусу R = 33 от вершины, то есть за пределами пирамиды. Это решение отбрасываем.
ответ: R₁ = (0 + 11√2)/√2 = 11.
угол DBC=30
угол DBC и угол ADB-накрест лежащие при BC//AD=30
В треугольнике против угла ADB лежит катет,равный 1/2 гипотенузы
AB=6см
Опускаем перпендикуляр СН и рассмотрим треугольник СHD :
угол НСD = 120 - 90 =30 градусов.
НD = 0,5*СD = 0.5 * 6 = 3см.
В треугольн. СНD по теореме Пифагора :
СН =5 см.
ВС = АD - 2 * НД= 12 - 6 = 6 см
S трапеции равна 0,5 * (12 + 6) * 5 = 45 см^2