ответ: Меньшая сторона = 5 см,
Большая сторона = 6 см.
Объяснение: Дан прямоугольник. S = 30 см²; P = 22 см.
Обозначим стороны прямоугольника а и b. Так как нам известны и площадь и периметр, то можно записать уравнения: S = a*b = 30 см²
и P = 2а + 2b = 22 см. Выразим из первого уравнения а = S/b = 30/b. Подставим это значение а во вторую формулу имеем:
2*30/b + 2b = 22 Решая уравнение относительно b имеем:
2b² - 22b + 60 = 0 b1 = 5см; b2 = 6 см Найденный два значения b являются искомыми сторонами прямоугольника. Но можно строго найти и стороны а1 = 30/5 = 6 см; а2 = 30/6 = 5 см.
Таким образом меньшая сторона прямоугольника = 5 см, Большая сторона = 6 см.
Проверим S = 5*6 = 30 см²
Р = 2*5 + 2*6 = 10 + 12 = 22 см.
Задача решена верно.
Условие задачи возможно, что намеренно - составлено некорректно.
Объяснение:
Условие задачи возможно, что намеренно - составлено некорректно. Если в параллелограмме известны стороны и высота, проведенная на одной из них, то длину второй высоты можно найти из его площади:
S=h×a, где h- высота, а- сторона, к которой она проведена. S=NH×KL => NQ-S:ML.
MNKL - параллелограмм => NK=ML=16. Тогда оказывается, что в треугольник NKH гипотенуза NK меньше катета NL (16 < 24), что противоречит относительно стороного прямоугольного треугольника.
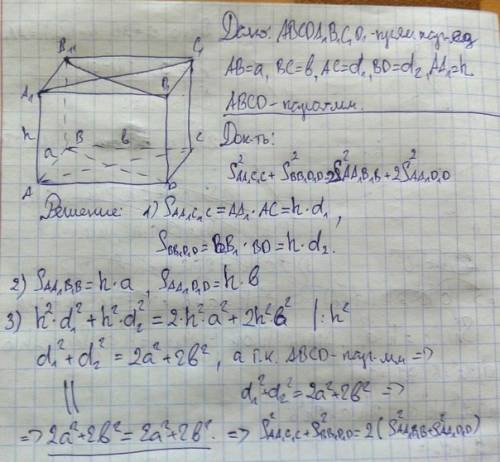
три диагональные сечения имеют стороны
a; корень( b^2+c^2)
b; корень( c^2+a^2)
c; корень( a^2+b^2)
сумма квадратов площадей трех диагональных сечений
S1 =(a* корень( b^2+c^2))^2+(b* корень( c^2+a^2))^2+(c* корень(a^2+b^2))^2=a^2( b^2+c^2)+b^2*( c^2+a^2)+c^2*(a^2+b^2)=2a^2b^2+2a^2c^2+2b^2c^2
сумма квадратов площадей всех его граней
S2=(a*b)^2*2+(b*c)^2*2+(c*a)^2*2=2a^2b^2+2a^2c^2+2b^2c^2
S1 = S2 - доказано