Явная опечатка. не 1 см, а 11 см. т.к. с такими данными не существует треугольника. исправьте условие.
теперь решение.
Если соединить середины сторон данного треугольника, то получите треугольник, состоящий их средних линий данного треугольника.
Каждая средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны, поэтому стороны треугольника, вершинами которого являются середины сторон данного треугольника, будут 5/2=2.5/см/, 7/2=3.5/см/, 11/2=5.5/см/
ответ 2.5см, 3.5 см, 5.5 см.
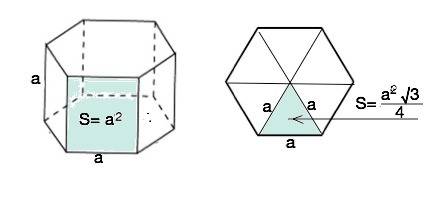
Каждое ребро правильной шестиугольной призмы равно а. Найдите площадь поверхности призмы.
---
Призма называется правильной, если ее боковые ребра перпендикулярны основаниям, а основания – правильные многоугольники.
Все ребра правильной призмы равны, ⇒
каждая из 6 боковых граней – квадрат, площадь которого S=a².
Ѕ(бок)=6а²
Основания правильной шестиугольной призмы - правильные шестиугольники, состоящие из 6 равных правильных треугольников.
Формула площади правильного треугольника S=(a²√3):4 ⇒
Ѕ (осн)•2=2•6•(a²√3):4=3а²√3
Площадь поверхности призмы равна сумме площадей: площади боковой поверхности и двух оснований.
S (призмы)= 6а²*+3•a²√3 или 3а²•(2+√3) ≈11,2а²