1)теугол. АВС-р/б(так как АС=ВС)
=> угол В=углу А=75 градусов
2) угол С=180-2угла А=30градусов
ответ:Угол С=30
2)Внешний угол при вершине В равен 155⁰, значит угол треугольника при вершине В равен 180⁰ - 155⁰ = 25⁰. Так как, АС = ВС, то треугольник равнобедренный и углы треугольника В и А равны, отсюда находим, что угол А равен 25⁰.
Так как, сумма углов треугольника равна 180⁰, то угол С равен 180⁰ - 25⁰ - 25⁰ = 130⁰.
ответ: угол С равен 130⁰.
3)АВС - равнобедренный треугольник, АВ=ВС, ∠CAB = ∠CBA.
Рассмотрим прямоугольный треугольник. ∠DBA = 90°-∠BAD=56°. Значит, ∠CAB = ∠CBA = 56°, тогда ∠ACB=180°-2*56°=68°.
На фотке это 4.

Объяснение:
1.
1)формула периметра та площі паралелограма
P=2(a+b)
S=ah, h - висота
2)формула периметра та площі прямокутника
P=2(a+b)
S=a* b
3)формула периметра та площі ромба
P=4a
S=ah
4)формула периметра та площі квадрата
P=4a
S=a²
2.
1. Знайдіть площу квадрата якщо його периметр становить 80см
Розвязання
периметр квадрата P=4a, знаходимо а
80=4а, а=80/4=20см - одна сторона квадрата
площа квадрата S=a² , 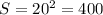 см
см
2. Знайдіть периметр прямокутника якщо його площа становить 98^2 а одна сторона удвічі більша за іншу
Розвязання
P=2(a+b) - периметр прямокутника
S=a* b - площа прямокутника,за умовою задачі b = 2*a нехай тоді одна сторона прямокутника дорівнює х а друга тоді буде 2х , моємо таке рівняння
2х*х=98
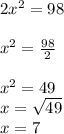
Тобто 1 сторона дорівнює 7 см, доті 2 сторона буде дорівнювати 7*2=14см
Знаходимо периметр
P=2(a+b)
Р=2(7+14)
Р= 42 см
ВСЕ
координаты вектора находятся как разность координат конца и начала вектора
2) Расстояние между точками B и D это длина вектора BD
Вектор BD( -6 - 5; -3 - (-2); 0 - 4) = (-11; -1; -4)
Длина вектора это квадратный корень из суммы квадратов координат вектора т.е.
3) Координаты середины отрезка это полусумма координат концов отрезка. Т.е.
точка М ( (-3+5)/2; (5 + (-2))/2 ; (-6+4)/2 ) = (1; 1,5; -1)
4) Произведение векторов AB и CD это сумма произведений их координат.
Сначала найдем вектора.
AB (5-(-3); -2-5; 4-(-6)) = (8;-7; 10)
CD (-6-0; -3-4; 0-3) = (-6; -7; -3)
Теперь перемножим координаты векторов и сложим их
AB * CD = 8*(-6) + (-7)*(-7) + 10*(-3) = -48+49-30 = -29
5) Угол между векторами можно найти из формулы векторного произведения векторов, которое равно произведению модулей векторов на косинус угла между ними.
Как уже было найдено в п4
AB (8;-7; 10) , CD (-6; -7; -3) и AB * CD = -29
Модуль |AB| равен
Модуль |CD| равен
Тогда
6) Аналогично пункту 5
Угол между векторами можно найти из формулы векторного произведения векторов, которое равно произведению модулей векторов на косинус угла между ними.
Как уже было найдено ранее
вектор AD (-3; -8; 6)
Найдем вектор ВС
Вектор ВС (0-5; 4-(-2); 3-4) = (-5; 6; -1)
Теперь найдем AD * ВС = (-3)*(-5) + (-8)*6 + 6*(-1) = -39
Модуль |AD| равен
Модуль |ВС| равен
Тогда
7) Вектор BD уже был найден BD(-11; -1; -4)
Вектор CB= - ВС = (5; -6; 1)
Найдем вектор AC (0-(-3); 4-5; 3-(-6) ) = (3; -1; 9)
Найдем сумму векторов AC и BD
AC(3; -1; 9) + BD(-11; -1; -4) = (3 + (-11); -1 + (-1); 9 + (-4) ) = (-8; -2; 5)
Теперь найдем произведение этого вектора на CB(5; -6; 1)
Произведение векторов равно (-8; -2; 5) * (5; -6; 1) = (-8)*5 + (-2)*(-6) + 5*1 = -23
8) Условие коллинеарности это пропроциональность координат векторов (если они не равны нулю)
В нашем случае AB(8;-7; 10) и CD(-6; -7; -3) не имеют нулевых координат, значит можно проверить на пропорциональность.
Очевидно
Следовательно вектора не коллинеарны.