Если три стороны одного треугольника соответственно пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Дано: ΔАВС, ΔА₁В₁С₁,
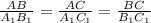
Доказать: ΔАВС подобен ΔА₁В₁С₁.
Доказательство:
На стороне АС треугольника АВС отложим СА₂ = С₁А₁ и проведем А₂В₂║АВ.
Так как прямая, параллельная стороне треугольника, отсекает треугольник, подобный данному, то
ΔАВС подобен ΔА₂В₂С , значит их стороны пропорциональны:
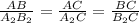 , а так как А₂С = А₁С₁, то получаем
, а так как А₂С = А₁С₁, то получаем
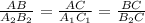 ,
,
По условию:
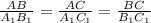 .
.
Из этих двух равенств следует, что
А₂В₂ = А₁В₁ и В₂С = В₁С₁.
Тогда ΔА₁В₁С₁ = ΔА₂В₂С по трем сторонам.
Значит,
ΔАВС подобен ΔА₁В₁С₁.
1) с)45 град
этт и без решения ясно 45 град
пояняю
наклонная -это гипотенуза
проекция-это катет1
раастояние от точки до плоскости катет2
катет1=катет2
равнобедренный,прямоугольный тругольник
основание гипотенуза-углы присоновании по 45 град
2 е)60
расстояние до плоскости - это перпендикуляр к плоскости - будет катет1 = 4 дм
расстояние от точки до прямой их пересечения -это гипотенуза = 8 дм
проекция гипотенузы на каждую плоскость - это катет2 - его длина не нужна
УГОЛ (пусть <a) между гипотенузой и катетом2 равен ПОЛОВИНЕ угла между плоскостями <A=2<a
тогда sin<a=катет1 / гипотенуза =4/8=1/2
sin<a=1/2 <это sin 30 град =1/2
<a=30
<A=2*<a=2*30=60 град