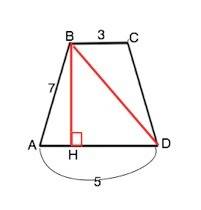
Проведем высоту ВН к большему основанию.
Высота равнобедренного треугольника, проведенная к большему основанию, делит его на отрезки, меньший из которых равен полуразности оснований, больший - их полусумме.
АН=(AD-BC):2=1
HD=(BC+AD):2=4
Из прямоугольного ∆ АВН по т.Пифагора высота
ВН=√(AB²-AH²)=√48=4√3
Из прямоугольного ∆ DBH диагональ
ВD=√(BH²+HD²)=√(48+16)=8 см (диагонали равнобедренной трапеции равны, ⇒ АС=8 см)
Площадь трапеции равна произведению высоты на полусумму оснований.
S=4√3•4=16√3 см*
А) проводим высоту, получаем треугольник, углы которого равны 90, 30 и 60
а в таком треугольнике катет против 30 градусов равен половине гипотенузы
то есть сторона А = 2*4=8 (сторона А, та которая сбоку)
периметр равен 2(А+В)=36, А=8
зачит В=(36-16)/2=10 см
площадь равна S=b*h= 10 *4=40
Б) в ромбе стороны равны
а*4=124
а=31
площадь равна половине произведения диагоналей
а вот дальше, я уже не знаю...