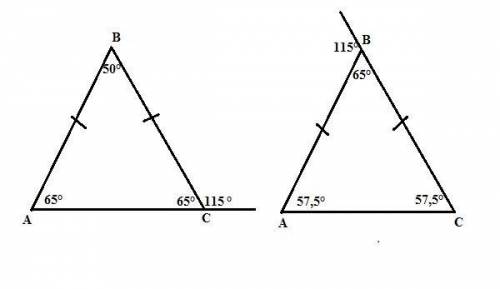
1. 65°, 65°, 50°.
2. 57,5°; 57,5°; 65°.
Объяснение:
Нам дан один из внешних углов равнобедренного треугольника. У равнобедренного треугольника углы при основании равны.
Значит возможны два варианта решения:
1. Если дан внешний угол при основании, то внутренний, смежный с ним, равен 180° - 115° = 65° (сумма смежных углов равна 180°).
Тогда угол при вершине треугольника равен 180° - 2·65° = 50° (по сумме внутренних углов треугольника, равной 180°).
ответ: 65°, 65°, 50°.
2. Если дан внешний угол при вершине, то внутренний, смежный с ним, равен 180° - 115° = 65° (сумма смежных углов равна 180°).
Внешний угол треугольника равен сумме двух внутренних (в нашем случае равных), не смежных с ним углов. Следовательно, углы при основании такого треугольника равны 115°:2 = 57,5°.
ответ: 57,5°; 57,5°; 65°.
20
Объяснение:
Рисунок я нарисовать не могу. Пусть ВС-малое основание, AD-большое основание р/б трапеции. Вписанная окружность касается сторон АВ, ВС, СD, AD в точках M,N,P,Q соответственно. Т.к. трапеция р.бокая, то AB=CD. BM=BN=CN=CP=1-по свойству касательных к окружности.
AM=AQ=DQ=DP=4-по свойству касательных к окружности. Отсюда ВС=1+1=2, AD=4+4=8
Проведем высоты ВВ1 и СС1 к AD. BC=B1C1=2. AB1=(AD-B1C1)/2=3
Тр-к ABB1-прямоугольный. по. Пифагора: BB1=sqrt(AB^2 - AB1^2)=sqrt(25-9)=4
S=1/2*(BC+AD)*BB1=1/2*(2+8)*4=20