Объяснение:
№5
Вариант 1.
По теореме: отрезки касательных, проведенные из одной точки к окружности, равны.
Исходя из этого:
АК=СК
ВК=DK
Так как
АВ=АК–ВК
СD=CK–KD
То:
АВ=СD.
Вариант 2.
Вариант 2.Проведём АС и BD.
По теореме: отрезки касательных, проведенные из одной точки к окружности, равны.
Тогда:
СК=АК
КВ=КD
Углы АКС и ВКD равны как вертикальные. Пусть каждый из них равен Y.
Рассмотрим треугольник АКС
СК=АК
Тогда треугольник равнобедренный с основанием АС.
Тогда угол АСК=(180–Y)÷2
Рассмотрим треугольник ВКD.
КВ=КD
Тогда треугольник равнобедренный с основанием BD
Тогда угол BDK=(180°–Y)÷2
Следовательно угол BDK=угол АСK.
Тогда АС||ВD, а углы BDC и АСD накрест-лежащие при параллельных прямых АС и ВD и секущей СD.
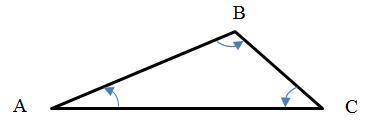
∠A=40°, ∠B=20°, ∠C=120°
Объяснение:
Дано:
ΔАВС (см. рисунок)
AB>BC>AC
один угол 120°
другой угол 40°
Найти: ∠A=?, ∠B=?, ∠C=?
Решение.
Сумма внутренних углов треугольника равна 180°. Зная значения двух углов находим третий угол Х:
Х+120°+40°=180°
Х=180°-160°=20°
Нам известно все три угла: 20°, 40°, 120°. Остается найти соответствие между значениями углов с углами ∠A, ∠B и ∠C.
Из теоремы косинусов следует, что в треугольнике наибольший угол лежит против наибольшей из сторон. Из AB>BC>AC следует, что наибольшая сторона - это АВ, то ∠C=120°, и наименьшая сторона - это АС, то ∠B=20°. Остается одно, ∠А=40°.
ответ: ∠A=40°, ∠B=20°, ∠C=120°
АО=ОВ (из условия)
СО=ОД (из условия)
угол АОД=углу СОВ (как вертикальные углы)
если эти треугольники равны значит равны и все элементы в них...значит АД=ВС доказано