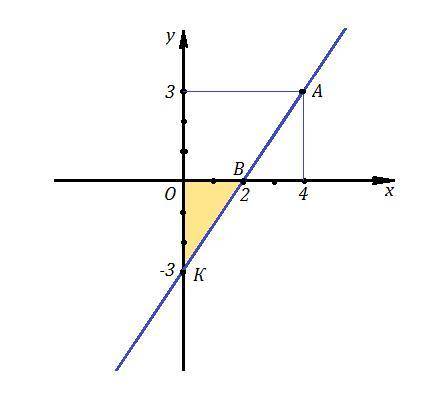
Рассмотрим вариант, когда прямая имеет угловой коэффициент k>0, тогда она наклонена к положительному направлению оси ОХ под острым углом. Из чертежа видно, что угол наклона не может быть тупым, т.к. тогда S треугольника будет больше 3 .
От координатного угла отсекается ΔВОК , площадь которого S=3. Это прямоугольный треугольник, его площадь равна половине произведения катетов., то есть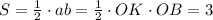 
.
Пусть ОК=3 ед. , а ОВ=2 ед. , тогда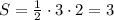 
.
Точка В в этом случае будет иметь координаты В(2,0), а точка К(0,-3) .
Подставим в уравнение прямой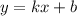 
координаты точки А(4,3) и , например, В(2,0), получим:
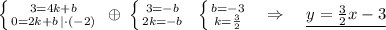
Или можно использовать то, что точка пересечения с осью ОУ имеет координаты К(0,-3). Тогда уравнение прямой имеет вид: y=kx-3 . И в это уравнение уже подставить координаты точки А(4,3) :
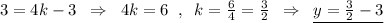
Также можно было составить уравнение прямой, проходящей через две точки А и В ( или А и К) .
Смотри рисунок.
8см
Объяснение:
угол A - 120 градусов и C столько же (это же ромб) и т.к. противолежащие углы равны то B и D тоже равны (по 60 градусов)
в ромбе диагонали являются также биссектрисами то есть углы abo и obc по 60/2=30 градусов
ближайшее расстояния до стороны перпендикулярный к ней отрезок
возьмем это на стороне BC точка F тогда угол BFO=90 градусов
BD-32 см а т.к. диагонали точкой пересечения пересекаются пополам то BO=OD=16 градусов
в треугольнике BFO BO-гипотенуза
а OBF-30 градусов
Если в прямоугольном треугольнике есть угол в 30 градусов то противолежащая ему сторона равна половине гипотенузы
то есть OF=BO/2
OF=16/2=8см
фух
Рассмотрим тр-ник АНВ. так как АН - высота, то он прямоугольный, угол АНВ - прямой. АВ = 8 см является гипотенузой этого тр-ка, АН = 4 см его катет.
Видно, что гипотенуза вдвое больше катета (АВ : АН = 8 : 4 = 2).
В прямоугольном тр-ке напротив угла 30 градусов лежит катет вдвое меньше гипотенузы, значит угол В = 30 градусов, тогда угол С = 90 - 30 = 60 градусов.
ответ: 60.