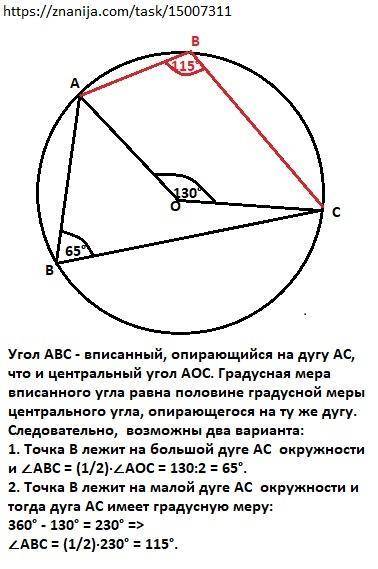
1. ∠АВС = 65°.
2. ∠АВС = 115°.
Объяснение:
Расположение точки В нам неизвестно, но предполагаем, что она находится на окружности.
Угол АВС - вписанный, опирающийся на дугу АС, что и центральный угол АОС. Градусная мера вписанного угла равна половине градусной меры центрального угла, опирающегося на ту же дугу. Градусная мера центрального угла равна градусной мере дуги, на которую он опирается.
Следовательно, возможны два варианта:
1. Точка В лежит на большой дуге АС окружности и
∠АВС = (1/2)·∠АОС = 130:2 = 65°.
2. Точка В лежит на малой дуге АС окружности и тогда дуга АС имеет градусную меру:
360° - 130° = 230° =>
∠АВС = (1/2)·230° = 115°.
β и удалены от линии их пересечения соответственно на 15 и 7 см. Найдите длины проекций отрезка АВ на данные плоскости.
-----------
Расстояние от точки до прямой - длина перпендикуляра, проведенного из этой точки к прямой.
Пусть точка А лежит в плоскости α, а точка В в плоскости β.
Тогда АС=15 см, а ВН=7 см.
Проекция АВ на плоскость α равна длине отрезка АН.
АН - наклонная к плоскости β. СН - ее проекция на плоскость β.
ВН ⊥ СН как расстояние от В до СН.
По т. о трех перпендикулярах прямая, проведенная в плоскости через основание наклонной перпендикулярно к её проекции на эту плоскость, перпендикулярна и к самой наклонной.
Треугольник АВН прямоугольный. Отношение катета ВН к гипотенузе АВ равно 3:5, и этот треугольник - египетский.
Значит, АН=20 ( можно проверить по т.Пифагора).
ВС - наклонная к плоскости α , СН ее проекция на плоскость α, и по т. о трех перпендикулярах ВС ⊥ АС, треугольник АВС прямоугольный. Отношение катета АС к гипотенузе ВС равно 7:25.
Этот треугольник из так называемых троек Пифагора, и ВС=24 см ( можно проверить по т.Пифагора).
Длины проекций отрезка АВ на данные плоскости. равны
20 см на плоскость α и 24 см на плоскость β.