Если в равнобедренной трапеции провести высоты ВН и СК, то получим НВСК - прямоугольник (ВС║КН, так как основания трапеции параллельны, ВН║СК как перпендикуляры к одной прямой), тогда
ВС = КН и ВН = СК.
ΔАВН = ΔDCK по гипотенузе и катету (АВ = CD, так как трапеция равнобедренная, ВН = СК), тогда
АН = DK = (AD - KH)/2 = (AD - BC)/2.
Площадь трапеции:
Sabcd = (AD + BC)/2 · BH
Воспользуемся этими выводами для решения задач:
а) AH = DK = (17 - 11)/2 = 3 см
ΔАВН прямоугольный с гипотенузой, равной 5 см и катетом 3 см, значит он египетский и
ВН = 4 см.
Sabcd = (17 + 11)/2 · 4 = 28/2 · 4 = 14 · 4 = 56 см²
б) AH = DK = (8 - 2)/2 = 3 см
ΔABH: ∠AHB = 90°, ∠BAH = 60°, ⇒ ∠ABH = 30°.
AB = 2AH = 6 см по свойству катета, лежащего напротив угла в 30°,
по теореме Пифагора:
BH = √(AB² - AH²) = √(36 - 9) = √27 = 3√3 см
Sabcd = (8 + 2)/2 · 3√3 = 15√3 см²
Объяснение:
1) Утверждение неверно.
Если площадь одного из подобных треугольников в 2 раза больше площади другого, то коэффициент подобия равен k = √2, потому что отношение площадей подобных треугольников равно квадрату коэффициента подобия.
2) Утверждение верно.
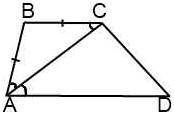
а) Если боковая сторона трапеции равна меньшему основанию, то диагональ его является биссектрисой острого угла, образованного большим основанием и этой боковой стороной.
Смотри прикреплённый рисунок 1.
Так как AB = BC, то Δ ABC — равнобедренный с основанием AC. Значит, ∠BAC = ∠BCA.
∠BCA = ∠CAD (накрест лежащие углы при AD ∥ BC и секущей AC).
Тогда ∠BAC = ∠CAD, и AC - биссектриса ∠BAD.
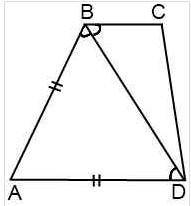
б) Если боковая сторона трапеции равна большему основанию, то диагональ его является биссектрисой тупого угла трапеции, образованного меньшим основанием и этой стороной.
Смотри прикреплённый рисунок 2.
АВ = АD и ΔABD — равнобедренный с основанием BD, его углы при основании равны ∠ABD = ∠ADB.
∠CBD = ∠ADB (накрест лежащие при AD ∥ BC и секущей BD).
Тогда ∠CBD=∠ABD, следовательно, BD — биссектриса ∠ABC.
3) Утверждение верно,
Вписанный угол АВС опирается на дугу окружности, равную 288°, а центральный угол АОС опирается на дугу окружности, равную 360 ° - 288° = 72°.
АС=2R·sin 30°=2R·(1/2)=R=12
По свойству пересекающихся хорд
АМ·МС=КМ·МВ
АМ=МС
КМ=2
6·6=2·MB
MB=18