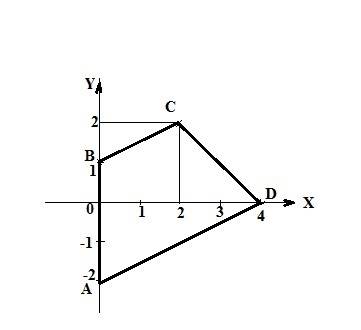
если все числа целые и периметр = 5, то стороны трапеции 1, 1, 1 и 2.
т.е. это равнобокая трапеция, у которой углы при основаниях равны.
Пусть трапеция АВСD, АВ и СD - бока =1 каждая, ВС - малое основание =1, AD - большое основание =2.
Из точки В опустим высоту BH
Рассмотрим полученный треугольник АВН
АВ=1
АН = (AD-ВС)/2=0,5
косинус угла А = АН/АВ = 0,5
следовательно, угол А=60градусов.
Угол D = углу А, т.к. трапеция равнобокая
следовательно сумма углов при большем основании (т.е. А и D) = 120
ответ: Г
формула объема пирамиды: V=hS/3 (треть высоты на основание), найду для начала вторую сторону прямоугольника. высота-есть катет, боковое ребро-есть гипотенуза, половина диагонали прямоугольника-это другой катет, его найду через теорему пифагора: 625-576=49-это квадрат половины диагонали, откуда найдем ее длину-7. Длина диагонали равна 2*7=14
найдя диагональ, найду вторую сторону прямоугольника так же через теорему пифагора, 196-169=27, откуда вторая сторона равна 3корня из 3
дальше площадь S основания пирамиды равна 13*3 корня из 3, то есть =39 корней из трех
подставлю все в формулу и получу: V= 1/3 * 39 корней из 3 * 24= 312 корней из 3