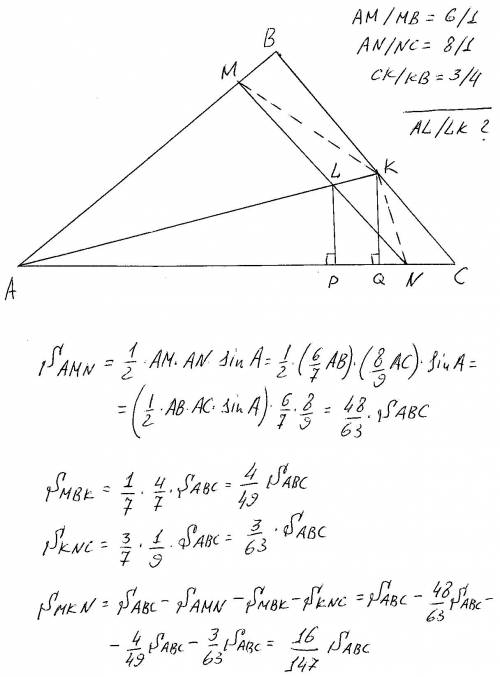
Обозначим треугольник АВС(смотри рисунок). Проведём перпендикуляры KQ и LP .Находим площадь треугольника AMN через площадь треугольника АВС. Аналогично находим площади всех нужных внутренних треугольников выражая их через площадь треугольника АВС. Площади треугольников MKL и NKL относятся также как и площади AMK и AKN, поскольку у них основание LK общее, а отношение высот равно отношению высот треугольников AMK и AKN. У треугольников AKN и ALN общее основание AN. Следовательно отношение их высот KQ и LP будет равно отношению их площадей=8/7. Но прямоугольные треугольники AKQ и ALP подобны, значит также и отношение AK/AL=8/7. ответ AL/LK=7/1.
Дано: < 1+ < 2 = < 3 ; < 1, < 2 - вертикальные; < 3 - смежный.
Найти: < 1 и < 2
Пусть х градусов - вертикальный <1 , тогда сумма их равна 2х,
(< 1 + < 2 = 2x)
сумма вертикальных по условию равна смежному углу, значит 2х градуса - смежный угол. ( 2x=< 3)
Сумма смежных углов равна 180 градусов.
Получаем уравнение:
х+2х=180*
3х=180*
х= 180:3
х=60 градусов каждый из вертикальных углов
ответ: < 1= 60 градусов;< 2 = 60 градусов
P/S. < - это если че, знак угла), а это * - знак градуса)))
О1 С1-перпендикуляр к большей хорде(24см)
Они делят хорды пополамИз прямоугольных треугольников пот.Пифагора находим
ОС=√(13^2-6^2)=√(169-25)=√144=12; R=26/2=13
O1C1=√(169-144)=√25=5
C1K перпендикуляр на ОС1; КС=ОС-О1С1; ОС1=12-5=7(см)
из прям. треугольникаКСС1 tga=21/7=3
Но там можно и по-другому нарисовать! Разберитесь с этим решением