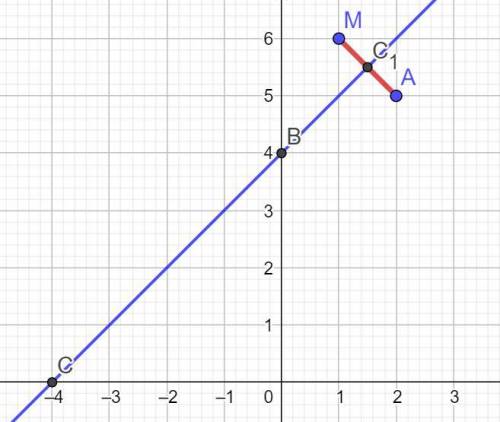
Геометрическое место точек, равно удалённых от точек А и В - это срединный перпендикуляр к отрезку АМ.
Пусть точка пересечения этого перпендикуляра с осью Оу (ось ординат) - это точка В(0; у).
Векторы: АВ = (0-2=-2; (у-5)) = (-2; (у-5)),
МВ = (0-1=-1; (у-6)) = (-1; (у-6)).
Расстояния: АВ² = 4 + у² - 10у + 25 = у² - 10у + 29.
МВ² = 1 + у² - 12у + 36 = у² - 12у + 37.
Приравняем: у² - 10у + 29 = у² - 12у + 37.
Отсюда 2у = 8, у = 8/2 = 4.
ответ: точка В(0; 4).
Пусть АВСД- трапеция. В ней ВС║АД, проведем СК║ВД, получим параллелограмм ВСКД, ДК=4, СК=13, треуг. АСК состоит из треугольников АСД И СДК. Сравним площади треуг. АВС и ДСК, в них одинаковые высоты и основания по 4 см. Поэтому они равновелики, Значит, площадть трапеции, можно заменить площадью треугольника АСК. найдем его площадь по формуле Герона, в нем полупериметр (13+14+15)/2=21, а площадь √(21*6*8*7)=84/см²/
ответ 84 см²