Всё в разделе "Объяснение".
Объяснение:1. Неверно.
Два треугольника называются подобными , если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.2. Верно.
Это 2 признак подобия треугольников.
3. Верно.
Даны два квадрата. Назовём их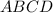 
и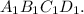 
Проведём диагональ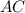 
в квадрате 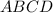и диагональ 
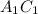в квадрате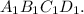
Рассмотрим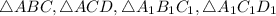 
.
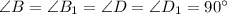, по свойству квадрата.
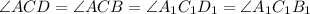, так как диагонали квадрата делят углы пополам.
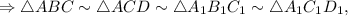по 1 признаку подобия треугольников.
4. Неверно.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.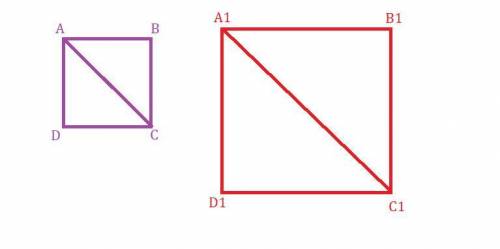
1) Чертим и отмечаем то, что нам известно
2) Здесь мы опускаем высоту CD, которая в равнобедренном треугольнике является и медианой, то есть делит сторону AB на две равные части AD и DB.
3) Находим углы при основании. Поскольку треугольник равнобедренный, то ∠A=∠B.
Так же мы сразу видим, что у нас есть 2 прямоугольных треугольника ΔADC и ΔCDB.
4)Когда мы нашли ∠A и ∠B, то с тангенса выражаем высоту, через половину длины основания.
5) Подставляем высоту, выраженную через половину длины основания и тангенса угла, в формулу площади равнобедренного треугольника и, таким образом, вычисляем чему равно основание AB.
6)Теперь в формуле площади ΔACB у нас неизвестная только одна высота CD. Мы можем её найти, что мы и делаем.
7) (На картинке данный пункт отмечен номером 6, как и предыдущий. Опечатка.)
Поскольку ΔADC и ΔCDB прямоугольны, то стороны AC и CB являются их гипотенузами, которые равны, так как ΔABC равнобедренный.
По теореме Пифагора находим их.
8) Записываем ответ.
Надеюсь, что доступно и понятно.