Построим отрезок BC длины a. Центр O описанной окружности треугольника ABC является точкой пересечения двух окружностей радиуса R с центрами в точках B и C. Выберем одну из этих точек пересечения и построим описанную окружность S треугольника ABC. Точка A является точкой пересечения окружности S к прямой, параллельной прямой BC и отстоящей от нее на расстояние ha (таких прямых две).
8.2.
Построим точки A1 и B1 на сторонах BC и AC соответственно так, что BA1 : A1C = 1 : 3 и AB1 : B1C = 1 : 2. Пусть точка X лежит внутри треугольника ABC. Ясно, что SABX : SBCX = 1 : 2 тогда и только тогда, когда точка X лежит на отрезке BB1, и SABX : SACX = 1 : 3 тогда и только тогда, когда точка X лежит на отрезке AA1. Поэтому искомая точка M является точкой пересечения отрезков AA1 и BB1.
8.3.
Пусть O — центр данной окружности, AB — хорда, проходящая через точку P, M — середина AB. Тогда |AP – BP| = 2PM. Так как РPMO = 90°, точка M лежит на окружности S с диаметром OP. Построим хорду PM окружности S так, что PM = a/2 (таких хорд две). Искомая хорда задается прямой PM.
8.4.
Пусть R — радиус данной окружности, O — ее центр. Центр искомой окружности лежит на окружности S радиуса |R ± r| с центром O. С другой стороны, ее центр лежит на прямой l, параллельной данной прямой и удаленной от нее на расстояние r (таких прямых две). Любая точка пересечения окружности S и прямой l может служить центром искомой окружности.
8.5.
Пусть R — радиус окружности S, O — ее центр. Если окружность S высекает на прямой, проходящей через точку A, хорду PQ и M — середина PQ, то OM2 = OQ2 – MQ2 = R2 – d2/4. Поэтому искомая прямая касается окружности радиуса
Ц
R2 – d2/4
с центром O.
8.6.
Возьмем на прямых AB и CD точки E и F так, чтобы прямые BF и CE имели заданные направления. Рассмотрим всевозможные параллелограммы PQRS с заданными направлениями сторон, вершины P и R которых лежат на лучах BA и CD, а вершина Q — на стороне BC (рис. 8.1). Докажем, что геометрическим местом вершин S является отрезок EF. В самом деле,
SR
EC
= PQ
EC
= BQ
BC
= FR
FC
, т. е. точка S
Объяснение:
1) Утверждение неверно.
Если площадь одного из подобных треугольников в 2 раза больше площади другого, то коэффициент подобия равен k = √2, потому что отношение площадей подобных треугольников равно квадрату коэффициента подобия.
2) Утверждение верно.
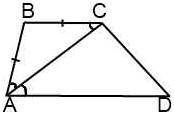
а) Если боковая сторона трапеции равна меньшему основанию, то диагональ его является биссектрисой острого угла, образованного большим основанием и этой боковой стороной.
Смотри прикреплённый рисунок 1.
Так как AB = BC, то Δ ABC — равнобедренный с основанием AC. Значит, ∠BAC = ∠BCA.
∠BCA = ∠CAD (накрест лежащие углы при AD ∥ BC и секущей AC).
Тогда ∠BAC = ∠CAD, и AC - биссектриса ∠BAD.
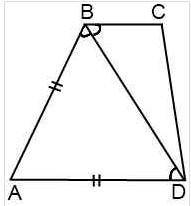
б) Если боковая сторона трапеции равна большему основанию, то диагональ его является биссектрисой тупого угла трапеции, образованного меньшим основанием и этой стороной.
Смотри прикреплённый рисунок 2.
АВ = АD и ΔABD — равнобедренный с основанием BD, его углы при основании равны ∠ABD = ∠ADB.
∠CBD = ∠ADB (накрест лежащие при AD ∥ BC и секущей BD).
Тогда ∠CBD=∠ABD, следовательно, BD — биссектриса ∠ABC.
3) Утверждение верно,
Вписанный угол АВС опирается на дугу окружности, равную 288°, а центральный угол АОС опирается на дугу окружности, равную 360 ° - 288° = 72°.
Минеральные ресурсы - это горные породы и минералы, которые используются или могут быть применены в народном хозяйстве: для получения энергии, в виде сырья, материалов и др.
Ресурсы Мирового океана — природные элементы, вещества и энергия, которые добывают или которые можно добывать непосредственно из вод, прибрежной суши, дна или недр океанов.
Земельные ресурсы - земли, которые находятся в границах территории РФ, за исключением территориального моря
Приро́дные ресу́рсы — это естественные ресурсы, необходимые для существования человеческого общества и используемые в хозяйстве.