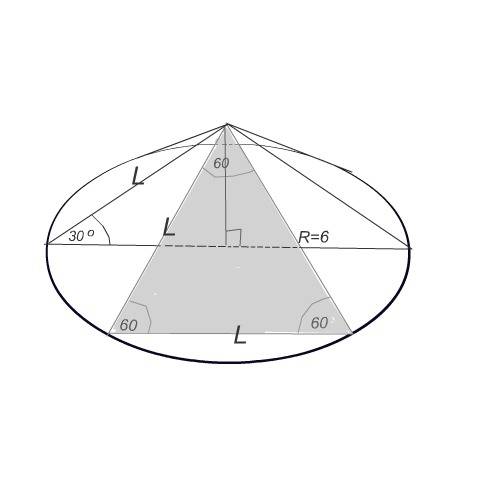
Образующая конуса наклонена к плоскости основания под углом 30°.
Плоскость сечения образована сторонами, равными образующей, и угол между ними 60°
Плоскость сечения - правильный треугольник.
Треугольник, образованный образующей, радиусом конуса и его высотой - половина правильного треугольника.
Высота - катет этого треугольника и равна половине образующей.
Второй катет равен радиусу основания и, как высота правильного треугольника
( можно и по теореме ПИфагора найти), равен (а√3):2=(L√3):2
(L√3):2=6
L√3=12 см
L=12:√3=12√3:√3*√3=12√3:3=4√3 см
Как уже сказано, плоскость сечения - равносторонний треугольник.
Формула площади равностороннего треугольника
S=(a²√3):4
S=(L√3)²√3:4=S=(16 *3)√3:4=48√3:4
S= 12√3 cм²
В параллелограмме противоположные углы равны, а смежные в сумме дают 180°.
Диагональ делить параллелограмм на два равных треугольника. Рассмотри один из таких треугольников, по условию два его угла равны 24° и 46°, тогда третий равен 180°-(24°+46°) = 180°-70° = 110° это один угол параллелограмма. Два смежных с ним угла равны 180°-110° = 70°. А противоположный ему угол, равен 110°.
ответ: 3) 70°, 70°, 110° и 110°.