периметр равен 13*4=52
площадь равна половине произведения диагоналей
площадь равна 24*10:2=120
Объяснение:
Дано: ромб АВСД
АВ=13 см, диогагаль АС =10
Найти:РАВСД -?, SАВСД-?
Стороны ромба равны,значит АВ=ВС=СД=АД=13см
Точка пересечения диоганалей -О
Рассмотрим треугольник АВО ,В котором АВ =13 см,ВО=5 см(диагональ точкой пересечения делится пополам)
периметр равен 13*4=52
площадь равна половине произведения диагоналей
площадь равна 24*10:2=120
ответ: Площадь ромба равна 120 см
Периметр равен 52 см
m || n
∠1 = 36˚
∠2 = 104˚
Найти:∠3
Решение:Вертикальные углы равны.
=> ∠1 = ∠4 = 36°, как вертикальные
При пересечении двух параллельных прямых секущей, накрест лежащие углы равны.
∠4 = ∠5 = 36°, как накрест лежащие.
Сумма углов треугольника равна 180°.
∠3 = 180° - (104° + 36°) = 40°
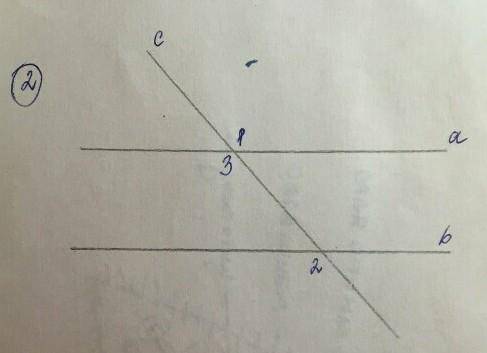
ответ: 40°Задача#2Дано:а || b
∠1 = 124°
Найти:∠2
Решение:Вертикальные углы равны.
=> ∠1 = ∠3 = 124°, как вертикальные.
При пересечении двух параллельных прямых секущей, соответственные углы равны.
=> ∠3 = ∠2 = 124°, как соответственные.
ответ: 124°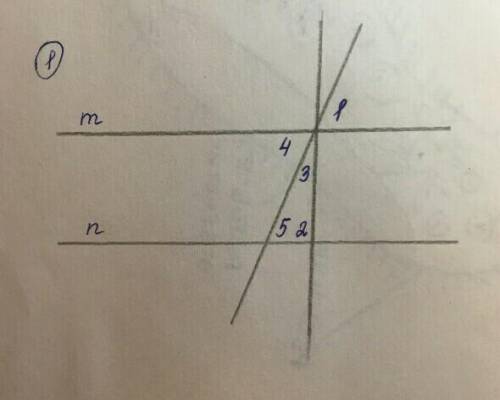
Пусть
х - АВ₁
(21 - х) - В₁С
Высота ВВ₁ разбивает ΔАВС на два прямоугольных треугольника ΔАВВ₁ и ΔВВ₁С
Для каждого из них применим теорему Пифагора и найдём катет ВВ₁,
В ΔАВВ₁
АВ² - АВ₁² = В₁В², т.е.
10² - х² = h²
В ΔВВ₁С
ВС² - В₁С² = В₁В² т.е.
17² - (21 - х)² = h²
Приравняем левые части выделенных равенств, получим уравнение
10² - х² = 17² - (21 - х)
100 - х² = 289 - 441 + 42х - х²
42х = 441 - 289 + 100
42х = 252
х = 252 : 42
х = 6 см - отрезок АВ₁
21 - 6 = 15 см - отрезок В₁С
h² = 100 - 6² = 100 - 36 = 64
h = √64 = 8 см
ответ: ВВ₁ = 8 см; АВ₁ = 6 см; В₁С = 15 см.