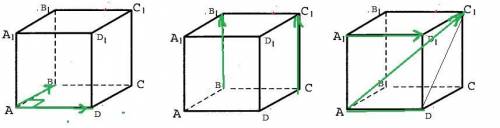
В кубе ABCDA1B1C1D1 найдите угол между векторами:
a)AB и AD , б)BB1 и CC1 , в)AC1 и A1D1
Объяснение:
Углы между векторами а)∠АВ,АD=90°, т.к все грани куба являются квадратами.
б) ∠ВВ₁,СС₁=0°, т.к эти вектора лежат на параллельных прямых.
в) ∠АС₁,А₁D₁=arcctg√2.
Т.к. вектор А₁D₁=AD , то найдем угол ∠АС₁,АD
Из ΔВСС₁ -прямоугольный. Пусть ребро куба а, тогда по т. Пифагора
ВС₁=а√2.
По т. о трех перпендикулярах если проекция ВС перпендикулярна , прямой лежащей в плоскости АВ, то и наклонная С₁В перпендикулярна прямой лежащей в плоскости АВ⇒ ΔАВС₁-прямоугольный .
tg∠С₁FD=BС₁/AB или tg∠С₁FD=а√2/а , tg∠С₁FD=√2 , ∠С₁FD=arctg√2,
а значит у угол между векторами ∠АС₁,А₁D₁=arcctg√2.
14) Найдите | 2а-в| , если | а|=3, | в|=4, а*в=4.
15) Длины векторов а и в равны 3 и 4 соответственно . Чему может равняться | 2а-в| : 0; 6 ; 1; 11 ?
22) Укажите уравнение прямой , чтобы точки А(а;-1) ,В(1-а ;2а+1) ,С(а+1;-3) лежали на одной прямой?
Объяснение:
14)
а*в=| а|*| в|*cos(∠а,в), значит 4=3*4*cos(∠а,в), или cos(∠а,в)=1/3
Тогда длину | 2а-в| можно найти по т. косинусов , т.к ∠(а,в)=∠(2а,в) , см. на чертеже.
| 2а-в| = | КР| , | 2а| = | ОК| , | в| = | ОР|
КР²=ОК²+ОР²-2*ОК*ОР*cos∠(2а,в) ,
КР²=6²+4²-2*6*4*1/3 ,
КР²=52-16 , КР²=36 , ⇒КР=6 ,| 2а-в| =6 .
15) доделаю
16) Условие при котором три точки А(х₁;у₁) , В(х₂;у₂) , С(х₃;у₃) лежат на одной прямой :(у₃-у₁):(у₂-у₁)=(х₃-х₁):(х₂-х₁).
Подставляем координаты А(а;-1) ,В(1-а ;2а+1) ,С(а+1;-3) :
(-3+1):(2а+1+1)=(а+1-а):(1-а-а) или -2:(2а+2)=1:(1-2а) или 2а+2=-2+4а или а=2. Тогда А(2;-1) ,В(-1 ;5)
Уравнение( каноническое) прямой проходящей через А(х₁;у₁) , В(х₂;у₂) : (х-х₁):(х₂-х₁)=(у-у₁):(у₂-у₁).
Подставим (х-2):(-1-2)=(у+1):(5+1) , получим 2(х-2)=-1(у+1) или
у=3-2х или у=-2х+3
Высота у треугольников АВР и ВРС общая, значит, точка Р делит площадь треугольника АВС на два в отношении 2:3
Площадь одной части этого отношения равна 35:(2+3)=7, и площадь
∆ АВР=2*7=14
Пусть в треугольнике АВР точка пересечения биссектрисы АК и отрезка ВР будет Н.
Так как ВН=НР, АН - медиана и делит площадь ∆АВР пополам (свойство).
Тогда площадь ∆ АВН=14:2=7
Биссектриса угла треугольника делит противоположную углу сторону в отношении прилежащих сторон (свойство). ⇒
Так как АВ:АС=2:5, то ВК:КС= 2:5
Высота из А в треугольниках АВК и АКС одна и та же, следовательно, площади треугольников АВК и АКС относятся как 2:5.
Отсюда площадь ∆ АВК=35:(2+5)*2=10
Т.к. площадь АВН=7, то Ѕ ∆ ВНК=Ѕ ∆ АВК-Ѕ ∆ АВН=10-7=3
В треугольнике ВРО отрезок НК || РО, и ВН=НР, поэтому НК его средняя линия. Треугольники ВНК иВРО подобны, k=1/2.
Отношение площадей подобных треугольников равно квадрату их коэффициента подобия.⇒
Ѕ∆ ВНК:Ѕ ∆ ВРО=k²=1/4
Тогда площадь ∆ ВОР=4 площади ВНК и равна 3*4=12
Площадь четырехугольника АВОР равна
Ѕ ∆ АВР+Ѕ ∆ВРО=14+12=26 (ед. площади)