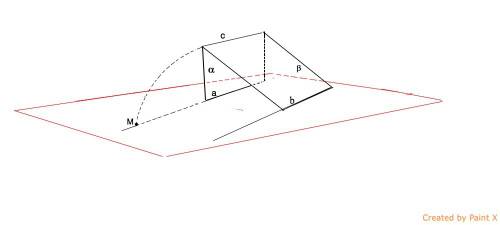
Параллельные прямые a и b лежат в плоскости гамма. Через прямую a проведена плоскость альфа, а через прямую b - плоскость бета так, что плоскости альфа и бета пересекаются по прямой c. Докажите, что c параллельна гамма.
-------------
1) Если через каждую из двух параллельных прямых проведена плоскость, причем эти плоскости пересекаются, то линия их пересечения параллельна каждой из данных прямых.
⇒ с || а и с || b
2) Если прямая, не лежащая в плоскости, параллельна некоторой прямой, лежащей в этой плоскости, то данная прямая параллельна самой плоскости
Прямая с, по которой пересекаются плоскости α и β, не лежит в плоскости гамма и параллельна а, лежащей в этой плоскости (см.п1). Требуется доказать п.2, т.е. что прямая с параллельна плоскости гамма.
Плоскость α содержит прямые с и а (с || а- см п.1).
Предположим, что прямая с пересекает плоскость гамма в точке М.
Тогда точка М принадлежит и плоскости гамма, и плоскости α, т.е. точка М принадлежит прямой а, содержащей линию, по которой плоскости α и гамма пересекаются. Получается, что прямые с и а пересекаются, что противоречит п.1.
(аналогично требуемое доказывается через прямую b).
Следовательно, с || гамма, ч.т.д.
Соответственно и основания трех треугольников будут относиться как 1:2:3 (по т. Фалеса)
если второе основание =2см ( а он состоит из 2-х частей) , тогда одна часть =1см, соответственно два других основания равны 1 и 3 см.
P.S. специально не решал геометрически, т.к. это наиболее доступное решение.