ответ:7√2
Объяснение:
Радиус вписаного круга, тоесть r
=a4/2 a4=56√2/4=14√2
14√2/2=7√2
Две окружности ,вписанные в угол ,касаются друг друга внешним образом .Центральный угол в 120° большей окружности , составленный из радиусов проведенных в точки касания ,стягивает дугу 15 см. Найти длину малой окружности.
Объяснение:
Пусть ОА=ОМ=R , CM=CK=r . По формуле длины дуги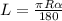 
,
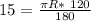⇒ R=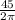 
см. По свойству отрезков касательных ∠АОР=60° .
Пусть СН⊥ОА , тогда ∠НСО=30°.
В ΔНСО по свойству угла 30° : ОС=2*ОН , но ОС=R+r , ОН=R-r ,
тогда R+r=2(R-r) → r=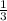 
*R → r= 
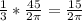(см) .
Длина окружности С=2πr , тогда С=2π*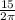 
=15 (см) .
Правильний чотирикутник, в який можна вписати коло, - це квадрат.
Сторона квадрата а=56√2/4=14√2 см.
Діаметр кола дорівнює довжині сторони квадрата, а радіус - половині довжини сторони квадрата, тобто
r=a/2=14√2/2=7√2 см.
Відповідь: 7√2 см.