10°
Объяснение:
Решение в приложении

KB = 10
Объяснение:
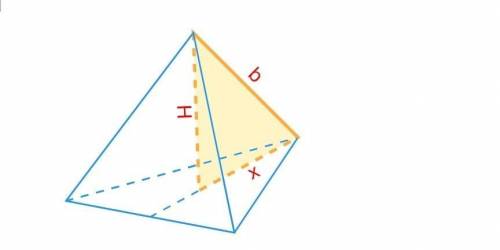
Судя по описанию, это - правильная треугольная пирамида.
Нам нужно найти боковое ребро пирамиды
(см. рисунок)
Для начала найдём расстояние от центра треугольника, до любой из его вершин с формулы для нахождения радиуса описанной около правильного треугольника окружности:
R=a/√3 , где a - сторона, равная по условию 6√3
Подставляем R=6√3/√3 = 6 - наш нижний катет прямоугольного треугольника KOB(к примеру)
Теперь нам известны два катета: KO или высота = 8,
OB = 6
Найдём гипотенузу KB с теоремы Пифагора:
KB=√(6²+8²) = √(36+64) = √100 = 10
З умови задачі нам відомо, що кут при вершині одного трикутнику, дорівнює куту при вершині іншого. Також ми знаємо, що ці трикутники рівнобедрені. Р одного трикутника дорівнює 30 см, тоді Р іншого трикутника, також дорівнює 30 см. Основа відноситься к бічній стороні як 1 : 2. складемо рівняння.
2х+х+2х (бічні сторони рівні) = 30 см
5х = 30 см
х = 6 см
Звідси виходить, що бічні сторони (2х) дорівнюють 12 см (2×6)
Відповідь: основа (а) = 6 см, бічні сторони (b,c) = 12 см.
P.S Прости если будет не правельно
ИЛИ
2) ΔВЕС; ∠5=90°-50°=40° (по свойству острых углов прямоуг. Δ)
3) ∠5=∠6 ( у прямоугольника диагонали равны и точкой пересечения делятся пополам); Δ ВОС равнобедр. Углы при основании равны)
4) ∠7=∠2-∠6=50-40=10°