они действительно равны
Объяснение:
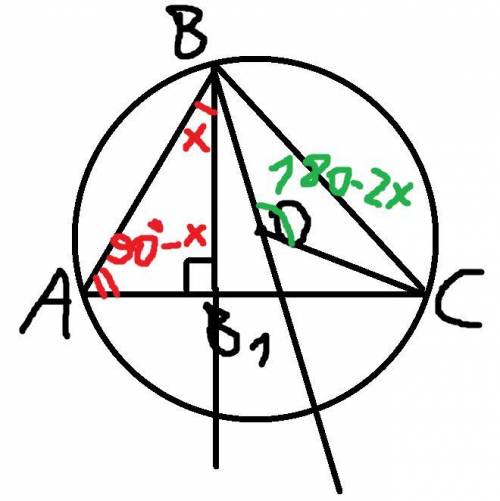
Пусть <ABB1 = x, тогда если <BB1A = 90 градусов (т.к. BB1 - высота), то ABB1 = (180 - 90 - x) градусов = (90 - x) градусов. Т.к. <BAC - вписанный для дуги BC, а <BOC - центральный для этой же дуги BC, то <BOC = 2*<BAC = 2*(90 - x)градусов = (180 - 2x) градусов. Очевидно, что BO = OC = R, тогда треугольник BOC - равнобедренный, тогда <CBO = <BCO = (180 - < BOC) / 2 = (180 - (180 - 2x)) / 2 = 2x / 2 = x. Следовательно <ABB1 = <CBO = x.
Так как 5² + 12² = 13², то треугольник АВС прямоугольный по теореме, обратной теореме Пифагора.
Его площадь:
S = 1/2 AB·AC = 1/2 BC·AK
S = 1/2 · 12 · 5 = 30 см²
1/2 · BC · AK = 30
BC · AK = 60
AK = 60/13 см