а) AM= 6, BM=9
б) r=4,5
Объяснение:
Для того чтобы не запутаться: n-BC, d-AC, m-AB.
Это на каких сторонах находятся точки.
1. Найдем третью сторону треугольника:
P=a+b+c
bc=48-(15+15)=18
2. Поскольку треугольник равнобедренный, точка касания, делит сторону BС на два равных отрезка:
BN=NC=9
3. По свойству касательных к окружности:
BN=NC=9
AM=AB-BM
(BM будет равно BN)
AM=15-9=6
4. Радиум можно будет найти по формуле площади:
r=
(p-полупериметр)
S=
Ну или же:

(AD-высота, ее можно найти по теореме Пифагора: AD=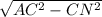 ; AD=
; AD=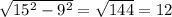 )
)
S=12*9=108
p=48:2=24
r=108:24=4,5
Брусок был подвергнут давлению по всем граням таким образом, что форма прямоугольного параллелепипеда сохранилась, но каждое ребро уменьшилось на 1 см.
Сравнивая два бруска, имеющих форму прямоугольного параллелепипеда, установили, что длина, ширина и высота второго бруска соответственно на 1 см больше, чем у первого бруска, а объем и полная поверхность второго бруска соответственно на 18 см3 и 30 см2 больше, чем у первого.
Одно из боковых ребер наклонного параллелепипеда составляет равные острые углы с прилежащими к нему сторонами нижнего основания.
Через диагональ нижнего основания произвольного параллелепипеда и середину не пересекающего ее бокового ребра проведена плоскость.
Как относятся объемы образовавшихся при этом частей параллелепипеда?
Дан параллелепипед ^SCDA^jCjDj.
Доказать, что в прямоугольном параллелепипеде ABCDA1B1C1D1 сумма.
1) Пусть Xf, хг и х3 — длины ребер, выходящих из одной вершины некоторого прямоугольного параллелепипеда.
2) Найти длины ребер такого прямоугольного параллелепипеда, у которого сумма всех ребер, полная поверхность и объем соответственно равны 48 см, 88 см2 и 48 см9.
Длины ребер, исходящих из общей вершины некоторого прямоугольного параллелепипеда, являются корнями уравнения а*3+ ~\-bx*-\-cx-}-d=Q.
Определить длину диагонали этого параллелепипеда.
Найти площадь поверхности сферы, описанной около прямоугольного параллелепипеда, три измерения которого являются корнями уравнения Х3+шг2+йлг+с=0.
] Доказать, что сумма квадратов длин всех ребер параллелепипеда равна сумме квадратов длин всех его четырех диагоналей.
Доказать, что из всех прямоугольных параллелепипедов С данной суммой всех ребер наибольший объем имеет куб.
Диагональ прямоугольного параллелепипеда рагаа 13 см, _а диагонали его боковых граней равны 4У10 см и 3]/17 см.
В прямом параллелепипеде стороны основания равны а и Ь, острый угол между ними содержит 60°.
Большая диагональ основания конгруэнтна меньшей диагонали параллелепипеда.
Основанием прямого параллелепипеда служит ромб.
В основании прямого параллелепипеда лежит параллелограмм со сторонами 1 см и 4 см и острым углом 60°.
Основанием параллелепипеда служит квадрат.
Определить полную поверхность этого параллелепипеда.
Определить объем прямоугольного параллелепипеда, диагональ которого равна / и составляет о одной гранью угол 30°, а с другой 45°.
Основанием прямого параллелепипеда служит ромб, площадь которого равна Q.
Стороны основания прямоугольного параллелепипеда равны а и Ь.
Стороны основания прямоугольного параллелепипеда равны а и Ь.
Определить объем прямоугольного параллелепипеда, если его диагональ равна d, а длины ребер относятся, как т: п: р.
В прямом параллелепипеде стороны основания равны а и Ь и образуют угол 30°.
Стороны основания прямоугольного параллелепипеда относятся, как т: п, а диагональное сечение представляет собой квадрат с площадью, равной Q.
Измерения прямоугольного параллелепипеда равны 2 см, 3 см и 6 см.
Из медной болванки, имеющей форму пря--моугольного параллелепипеда размером 80 смХ20 смХ Х5 см, прокатывается лист толщиной 1 мм.
В наклонном параллелепипеде проекция бокового ребра на плоскость основания равна 5 дм, а высота равна 12 дм.
Основанием параллелепипеда служит ромб со стороной а и острым углом 30