1) Сумма внешнего и внутреннего угла многоугольника равна 180° ⇒ следовательно внутренний угол многоугольника равен 180° - 20° = 160°
Величина внутреннего угла правильного многоугольника зависит от количества его сторон n и выражается формулой:
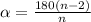
Найдем при каком n угол будет равен 160°:
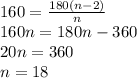
Т.е. угол в 160° будет у правильного 18-угольника
2) Радиус окружности описанной около правильного треугольника R и сторона a треугольника связаны соотношением:
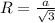
Подставим заданное значение стороны:
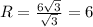
Следовательно, радиус окружности, описанной около этого треугольника равен 6 см
3) Градусная мера всей окружности равна 360°, а радианная мера 2π, следовательно градусная мера дуги равна:
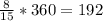 °
°
а радианная:

Длину дуги найдем как 8/15 от длины окружности:
 см
см
V = 720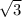 ≈ 1247,0766
≈ 1247,0766
Объяснение:
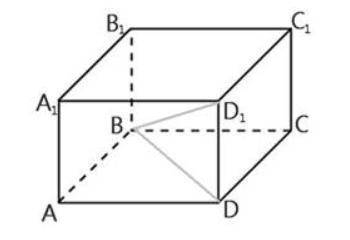
Треугольник ABD - прямоугольный.
Т.к. один его угол равен 30°, то второй угол = 180 - 90 = 60, т.е. это прямоугольный треугольник 30 60 90, а по его свойству, катет, противолежащий углу 30° (AD) равен половине гипотенузы (BD), т.е. гипотенуза BD равна:
BD = 2*AD = 2*12 = 24,
а катет, прилежащий углу 30° (AB) равен 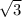 от противолежащего углу катета (AD), что доказывается теоремой Пифагора:
от противолежащего углу катета (AD), что доказывается теоремой Пифагора:
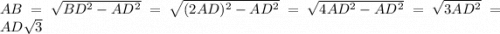
Итак:
AB = 12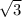 ;
;
Объем параллелепипеда равен произведению его сторон:
V = AA1 * AD * AB = 5 * 12 * 12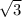 = 720
= 720
из этого:
а) ∠K=∠A=30°
б) отношение площадей подобных треугольников = коэффициент подобия в квадрате
SΔKMN:SΔABC=k²
SΔKMN:SΔABC=4
в) биссектриса делит сторону на отрезки, пропорциональные прилежащим сторонам.
Пусть биссектриса и ∠С - CD, тогда