Одну четвертую часть.
Можно решать по рисунку
ответ:Оба треугольника равнобедренные,т к АС=DB и точка О делит их пополам,т е
АО=О-В;DO=OC
Углы при основании равнобедренных треугольников равны между собой
<D=<C=60 градусов
Угол при вершине равен
<DOC=180-60•2=60 градусов
Как оказалось,все углы треугольника DOC равны по 60 градусов,значит треугольник даже не равнобедренный,а равносторонний
Треугольники DOC и АОВ равны между собой по первому признаку равенства треугольников
АО=ОС;ОB =ОD; по условию задачи
<DOC=<AOB,как вертикальные
Равенство треугольников доказано,поэтому все углы треугольника АОВ равны по 60 градусов
<ВАО=60 градусов
Объяснение:
Объяснение:
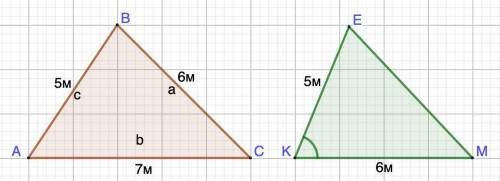
Дано: ΔАВС.
АВ = 5м; ВС = 6м; АС = 7м.
Найти: cos∠A; cos∠B; cos∠C
Для решения воспользуемся теоремой косинусов:
a² = b² + c² - 2 bc · cos∠A
1. Найдем cos∠A:
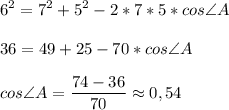
2. Найдем cos∠B:
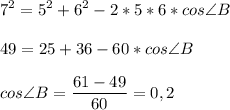
3. Найдем cos∠C:
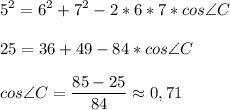
2) Дано: ΔКЕМ.
КЕ = 5 м; КМ = 6 м; sin∠K = 0,6
Найти: ЕМ
Воспользуемся теоремой косинусов. Но для этого нам нужен косинус, а нам дан синус.
Выразим косинус из основного тригонометрического тождества:
sin²α + cos²α = 1
Тогда имеем:
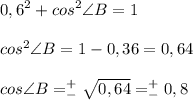
Так как в условии не сказано, острый это угол или тупой, то рассмотрим 2 варианта:
1. cos∠B = 0,8
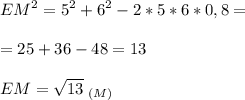
2. cos∠B = -0,8
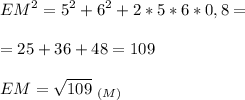
1\4, так как треугольники большой и тот, который в нем, будут подобными, и коэффициент подобия их сторон будет k = 1\2
а мы знаем, что площади подобных треугольников имеют k^2
а (1\2)^2 = 1\4