Основание прямой призмы abca1b1c1- равнобедренный треугольник, в котором ab=ac=10 см, bc=12 см. расстояние от вершины b до середины ребра а1с1 равно кв.корень из 353 см. найдите : а) площадь боковой поверхности призмы б) объём призмы

👇

Увидеть ответ

Ответ:

Lane9ig

17.03.2021

для начала най дем площадь основания:

Опустим высоту АК из вершины А., тогда

по т Пиф АК= корень из(100-36)=8см, тогда

Sоснования=1/2*8*12=48 см кв.

Середину А1С1 обозначим т.М, тогда А1М=МС1=5 см ( по условию ) и ВМ=корень из 353

Из треугольника ВМС: МС=корень из(353-144)=корень из 209

Из треугольника МСС1: С1С=корень из(209-25)=корень из184=2корня из46 - высота призмы

S А1В1ВА=S A1C1CA=10*2корня из46=20корней из 46

S СС1В1В= 12*2корня из46=24 корня из46

Sбок пов= 20корней из 46+20корней из 46+24 корня из46=64корня из 46 см кв.

V призмы=Sоснования * высоту=48*2корня из46=96корней из46 см кубич.

ответ: Площадь боковой поверхности = 64корня из 46 см кв

объём призмы = 96корней из46 см кубич.

Удачи ! )

4,6(70 оценок)

Открыть все ответы

Ответ:

krop40

17.03.2021

1. ABCD - сечение цилиндра, проведенное параллельно оси.
BD = 6 см, ∠BDA = 45°.
ΔBDA: ∠BAD = 90°, ∠BDA = 45°, ⇒ ∠DBA = 45°, ⇒
   BA = AD = x
   x² + x² = 6²
   2x² = 36
   x = √18 = 3√2
H = AB = 3√2 см - высота цилиндра.

Дуга AD 60°, ⇒ ∠AOD = 60° (центральный)
ΔAOD: AO = OD = R, ∠AOD = 60°, ⇒ треугольник равносторонний.
R = AD = 3√2 см

Sбок = 2πRH = 2π· 3√2· 3√2 = 36π см²

2. ВО = 6 см - высота конуса,
ОС = 2√3 дм - радиус основания.
ΔВОС: ∠ВОС = 90°, по теореме Пифагора
      ВС = √(ВО² + ОС²) = √(0,36 + 12) = √12,36 дм

Сечение ΔАВС - равносторонний, так как АВ = ВС как образующие, ∠АВС = 60°.
Sabc = a²√3/4, где а - сторона равностороннего треугольника.
Sabc = 12,36√3/4 = 3,09√3 дм²

4,4(38 оценок)

Ответ:

eremenko6kirov

17.03.2021

Фактически задача сводится к нахождению координат вектора CD.

Мы знаем, что СD перпендикулярно AB. И CD проходит через точку C.

Условие перпендикулярности -> косинус угла между векторами CD и AB равен нулю.

Формула косинуса угла между векторами - $cos(AB\ \^;CD)=\frac{x_{1}x_{2}+y_{1}y_{2}}{\sqrt{x_{1}^{2}+y_{1}^{2}}\sqrt{x_{2}^{2}+y_{2}^{2}}}$

AB={-1+5;4-1}={4;3}

CD={x2-3;y2-2}

Составим уравнение прямой АВ: $\frac{x+1}{4}=\frac{y-4}{3}$ (*)

Подставляя вместо x1 и y1 в формулу косинуса 4 и 3 соответственно получим:

4(x2-3)+3(y2-2)=0

Также точка D принадлежит прямой AB, а значит x2 и y2 удовлетворяют уравнению (*).

Решаем полученную систему уравнений.

$\left \{ {{4(x2-3)+3(y2-2)=0} \atop {\frac{x2+1}{4}=\frac{y2-4}{3}}} \right.$

Мне лень решать - сами решите. Как найдёте x2 и y2 - подставьте их и найдите координаты вектора CD. Зная координаты направляющего вектора и точку, через которую проходит прямая, легко составить уравнение прямой.

Оно выглядит так: 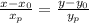$\frac{x-x_{0}}{x_{p}}=\frac{y-y_{0}}{y_{p}}$ , где $x_{p}, y_{p}$ - координаты напрвляющего вектора (в нашем случае вектора CD), а х0 и у0 - координаты точки, через которую проходит прямая (в нашем случае С или D - на выбор)