DOA = 70°. Дано в задаче.
BOC = DOA = 70°. Вертикальные углы равны (1).
DOC = 180° - 70° - 110°. Смежные углы в сумме дают 180° (2).
AOB = DOC = 110°. (1).
ODC = (180° - 110°) / 2 = 35°. Сумма углов треугольника равна 180° (3). Если треугольник равнобедренный, то углы при его основаниях равны (4).
ADO = 90° - 35° = 55°. Два угла составляют прямой угол (5).
OAD = ADO = 55°. (4).
OAB = 90° - 55° = 35°. (5).
OBA = OAB = 35°. (4).
OBC = 90° - 35° = 55°. (5).
OCB = OBC = 55°. (4).
Все остальные углы состоят из других и их можно посчитать по сумме. Например:
DAB = DAO + BAO = 55° + 35° = 90°.
Здесь даже чертеж не нужен (хотя он для наглядности приложен)
Помним теорему синусов треугольника:
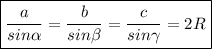
Где угол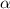 
лежит напротив стороны 
, угол 
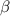лежит напротив стороны 
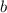, а угол 
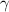лежит напротив стороны 
, а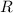 
- радиус описанной около треугольника окружности (правда, окружность в этой задаче нам не нужна)
Учитывая, что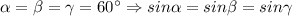 
Но тогда теорему синусов можно переписать так:
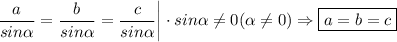
Что и требовалось доказать.
Можно ещё по-другому пойти.
Смотрим на рисунок.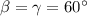 
(нижние углы), то есть треугольник равнобедренный с основанием , значит, боковые стороны равны, то есть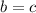 
Далее,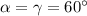 
, то треугольник равнобедренный с основанием 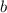, боковые стороны равны, то есть 
Ну и завершающий вывод:
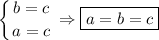
Что и требовалось доказать.
Площадь одного сектора: S' = S/6 = 4,71 (м²) = 471 (дм²)
Если для одного цветка необходимо 1 дм² земли,
то в каждом секторе можно посадить 471 цветок.
ответ: 471 цветок одного вида можно посадить на 1/6 клумбы