V = 720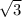
≈ 1247,0766
Объяснение:
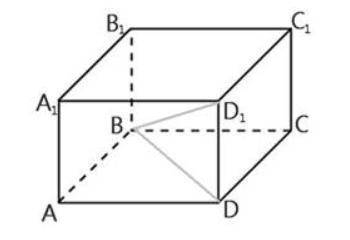
Треугольник ABD - прямоугольный.
Т.к. один его угол равен 30°, то второй угол = 180 - 90 = 60, т.е. это прямоугольный треугольник 30 60 90, а по его свойству, катет, противолежащий углу 30° (AD) равен половине гипотенузы (BD), т.е. гипотенуза BD равна:
BD = 2*AD = 2*12 = 24,
а катет, прилежащий углу 30° (AB) равен 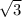от противолежащего углу катета (AD), что доказывается теоремой Пифагора:
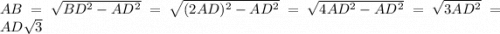
Итак:
AB = 12 ;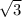
Объем параллелепипеда равен произведению его сторон:
V = AA1 * AD * AB = 5 * 12 * 12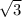 = 720
1. Зная, что медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2 : 1, считая от вершины, находим длину ВЕ:
ВЕ = ВО * 3 / 2 = 36 см, и ОЕ = 36 - 24 = 12 см
2. Рассмотрим треугольник АОЕ. Он прямоугольный, т.к. медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой. По теореме Пифагора найдем неизвестный катет АЕ, зная ОЕ и АО:
АЕ = √(9√2)² - 12² = √18 = 3√2
3. Получившиеся прямоугольные треугольники АЕВ и КОВ - подобные по первому признаку подобия (угол КОВ = АЕВ = 90°, угол АВЕ - общий). Значит:
= , КО = ;КО = = 2√2
Поскольку ВЕ - медиана, то КМ = КО*2; КМ = 2*2√2 = 4√2 см