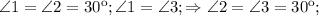 )
) 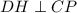 ,
, 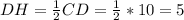 как катет лежащий против угла 30 в треугольнике CHD.
как катет лежащий против угла 30 в треугольнике CHD. 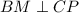 ,
, 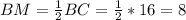 как катет лежащий против угла 30 в треугольнике BMC.
как катет лежащий против угла 30 в треугольнике BMC. 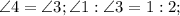
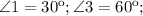 Тогда в ромбе
Тогда в ромбе 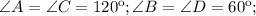
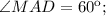 , тогда
, тогда 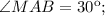 Треугольник BAM равнобедренный, АВ=АМ, тогда
Треугольник BAM равнобедренный, АВ=АМ, тогда 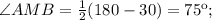
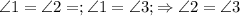 , треугольник MCD равнобедренный, MD=CD=3,
, треугольник MCD равнобедренный, MD=CD=3, 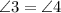 ,
, 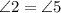 , как накрест лежащие при параллельных прямых АВ и CD, треугольник NAM равнобедренный, AM=AN=4.
, как накрест лежащие при параллельных прямых АВ и CD, треугольник NAM равнобедренный, AM=AN=4.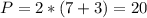 .
.
1 + ctg²a = 1 + cos²a / sin²a = (sin² a + cos² a) / sin² a = 1/sin² a
Известно, что тангенс угла ромба tg a = 8√17/17 => ctg a = 17/8/√17 = √17/8
1 + ctg²a = 1 + 17/64 = (64+17) / 64 = 81/64
1/sin²a = 81/64
sin² a = 64/81
sin a = 8/9
Площадь ромба S = a² * sin α, где а - сторона ромба, α - любой угол
Периметр ромба P = 4*a = 72 по условию.
а = 72/4 = 18
Получим S = a*a*sin α = 18*18*8/9 = 288