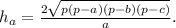
7.(2б)
Найти угол между стороной AB и медианой BB₁ треугольника ABC :
A(3; 5; 0) , B(0 ; - 6; 0) , C(3 ;1 ;0) . AB₁=CB₁ = AC/2 = 2
∠ABB₁ -?
- - - - - - - - - - --
B₁ (3 ; 3; 0) _середина стороны AC * * * (3+3) /2 ; (5+1)/2 ; (0+0)/2 * * *
BA { 3 ; 11 ; 0 } * * * 3 -0 ; 5 -(-6) ; 0 -0 * * *
BB₁ { 3 ; 9 ; 0 } * * * 3 -0 ; 3 -(-6) ; 0 -0 * * *
cos(∠(BA, BB₁) ) = BA*BB₁ / |BA|*|BB₁| =
(3*3+11*9 +0*0)/√(3²+11²+0²)*√(3²+9²+0²) =108/√130*√90 =
108/ 30 √13 =3,6 / √13 .
* * * ! 3,6 /√13 =(√3,6²) /√13 =√12,96 /√13 < 1 * * *
∠(BA, BB₁) =arccos(3,6 /√13 )
BA*BB₁ - скалярное произведение векторов BA и BB₁
|BA| и |BB₁| - модули векторов BA и BB₁
- - - - - - - -
8.(2б)
B(2 ; - 1; - 1) , A(2 ; 2 ; - 4) , C(3 ; - 1 ; -2) ,
BA { 0 ; 3 ; -3} ; BC { 1 ; 0 ; - 1}
cos(∠(BA, BC) ) = BA*BB / |BA|*|BC|
BA*BC - скалярное произведение векторов BA и BC
|BA| и |BC| - модули векторов BA и BC
* * * ∠(BA, BC) = ∠B * * *
cos∠B = cos(∠(BA, BC) )= (0*1+3*0 + (-3)*(-1) )/√(0²+3²+(-3)² )*√(1²+0²+(-1)²) =
3/√18*√2 = 3/6 =1/2 ⇒ ∠B =60 °
Внешний угол при вершине B будет 180° - ∠B = 180° - 60 ° = 120°
- - - - - - - -
9.(2б) Центр сферы A(4 ; -4 ; 2) , O(0 ; 0 ;0) ∈ поверхности сферы
* * *(x - x₀)²+(y - y₀)²+ (z - z₀)² = R² уравнение сферы радиусом R , центр которой в точке A( x₀; y₀ ; z₀) * * *
(x - 4)²+(y +4)²+ (z -2)² = R² Нужно найти R
Т.к. O(0 ; 0 ;0) ∈ поверхности сферы ,то
(0 - 4)²+(0 +4)²+ (0 -2)² = R² ⇔ R² =36
следовательно
(x - 4)²+(y +4)²+ (z -2)² = 36 * * * R² =6² * * *


надо найти сторону BH=BA/2=78V3/2=39V3
теперь по теореме Пифагора, находим сторону CH=все из под корня 78V3 в квадрате - 39V3 в квадрате=все из под корня 18252-4563= из под корня 13689 и равняется 117см