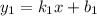 и
и 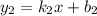 , будут перпендикулярны тогда и только тогда, когда
, будут перпендикулярны тогда и только тогда, когда 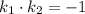 . Коэффициенты
. Коэффициенты 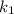 и
и 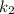 называются угловыми коэффициентами.
называются угловыми коэффициентами.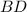 , которая лежит на прямой
, которая лежит на прямой 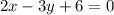 . Приведём уравнение этой прямой в нужный нам вид:
. Приведём уравнение этой прямой в нужный нам вид: 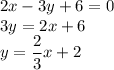 .
. 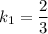 .
. 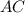 лежит на прямой
лежит на прямой 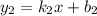 .Тогда, т.к. диагонали в квадрате перпендикулярны,
.Тогда, т.к. диагонали в квадрате перпендикулярны, 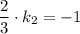 , откуда
, откуда 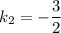 . Т.е диагональ
. Т.е диагональ 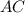 лежит на прямой
лежит на прямой 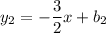 . Но мы также знаем, что эта прямая проходит через точку
. Но мы также знаем, что эта прямая проходит через точку 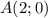 . Исходя из этого составим уравнение:
. Исходя из этого составим уравнение: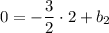 , откуда
, откуда 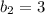 . Мы получили уравнение прямой, на которой лежит диагональ
. Мы получили уравнение прямой, на которой лежит диагональ 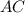 - это прямая
- это прямая 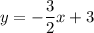 или, что то же самое,
или, что то же самое, 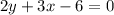 .
.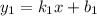 и
и 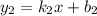 , пересекаются под углом
, пересекаются под углом 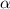 , тангенс которого равен
, тангенс которого равен 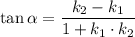 . Причём при
. Причём при 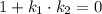 они перпендикулярны.
они перпендикулярны.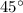 . Пусть сторона
. Пусть сторона 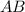 лежит на прямой
лежит на прямой 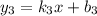 . Получается, нам нужно, чтобы прямая
. Получается, нам нужно, чтобы прямая 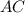 при пересечении с прямой
при пересечении с прямой 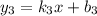 образовывала угол в
образовывала угол в 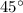 . (А сторона
. (А сторона 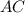 лежит на прямой
лежит на прямой 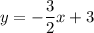 .)
.)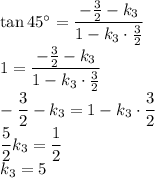
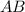 лежит на прямой
лежит на прямой 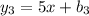 . Но мы также знаем, что эта прямая проходит через точку
. Но мы также знаем, что эта прямая проходит через точку 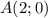 . Получаем, что
. Получаем, что 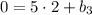 , откуда
, откуда 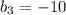 . Значит, сторона
. Значит, сторона 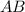 лежит на прямой
лежит на прямой  .
.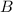 - это точка пересечения диагонали
- это точка пересечения диагонали 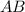 и стороны
и стороны 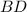 :
: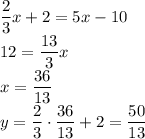

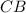 , имеет вид
, имеет вид 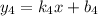 . Она перпендикулярна прямой, на которой лежит сторона
. Она перпендикулярна прямой, на которой лежит сторона 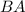 . Отсюда, по вышеприведённому методу, найдём уравнение прямой, на которой лежит сторона
. Отсюда, по вышеприведённому методу, найдём уравнение прямой, на которой лежит сторона 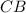 :
: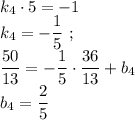
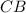 лежит на прямой
лежит на прямой 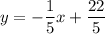 .
.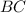 параллельна
параллельна 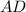 , отсюда следует, что угловые коэффициенты этих прямых равны. Находим уравнение прямой, на которой лежит сторона
, отсюда следует, что угловые коэффициенты этих прямых равны. Находим уравнение прямой, на которой лежит сторона 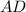 :
: 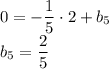
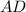 :
: 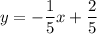 .
.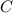 :
: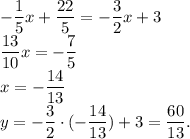
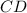 параллельна
параллельна 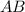 , отсюда следует, что угловые коэффициенты этих прямых равны. Находим уравнение стороны CD:
, отсюда следует, что угловые коэффициенты этих прямых равны. Находим уравнение стороны CD: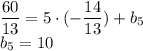
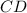 лежит на прямой
лежит на прямой 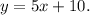
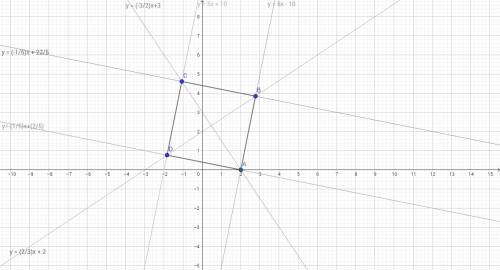
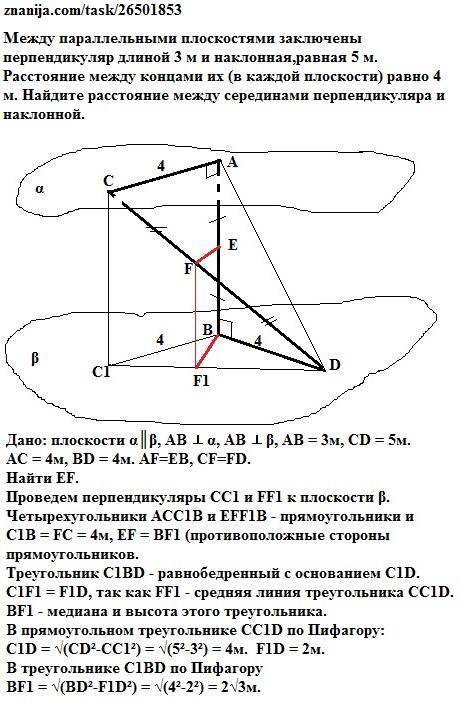
Расстояние между серединами перпендикуляра и наклонной равно 2√3 м.
Объяснение:
Дано: плоскости α║β, АВ ⊥ α, АВ ⊥ β, АВ = 3м, СD = 5м.
АС = 4м, BD = 4м. AF=EB, CF=FD.
Найти EF.
Проведем перпендикуляры СС1 и FF1 к плоскости β.
Четырехугольники АСС1В и EFF1B - прямоугольники и
C1B = FC = 4м, EF = BF1 (противоположные стороны прямоугольников.
Треугольник С1BD - равнобедренный с основанием С1D.
С1F1 = F1D, так как FF1 - средняя линия треугольника СС1D.
BF1 - медиана и высота этого треугольника.
В прямоугольном треугольнике CC1D по Пифагору:
C1D = √(CD²-CC1²) = √(5²-3²) = 4м. F1D = 2м.
В треугольнике С1BD по Пифагору
BF1 = √(BD²-F1D²) = √(4²-2²) = 2√3м.
EF = BF1 = 2√3 м.