В декартовой системе координат координаты вектора по заданным точкам определяется путём вычитания начальной точки из конечной и умножения на Декартовый коофициент соответственно (0,4)-(-3,0)=(3,4) (3,4)*2,65=(7,95,10,5) ЯДлинна находится соложением координат и делением на 2 7,95+10,5/2=9,225
9
9
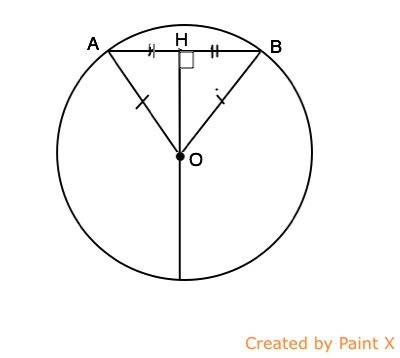
Соединим центр О окружности с концами хорды АВ. ОА=ОВ=R.
Треугольник АОВ - равнобедренный. Проведем высоту ОН этого треугольника.
Угол ОНВ=углу ОНА=90º
«Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один»
Следовательно, и к середине хорды можно провести только один перпендикуляр.
Высота ОН - медиана равнобедренного треугольника.
АН=ВН. Точка Н - середина АВ.
Следовательно, ОН, проходящий через середину АВ, есть срединный перпендикуляр хорды АВ, ч.т.д.
ab=((x2-x1)+(y2-y1))^1/2=(3^2+16)^1/2= 25^1/2=5