расстояние от точки до плоскости ромба 8см
Объяснение:
площадь ромба через синус любого угла
S=a²×sinα , отсюда сторона
а=√S/sinα= √(144√2÷sin45°)=√(144√2÷√2/2)=
√(144√2×2/√2)=√144×2=12√2 см
радиус вписанной окружности в ромб
r=S/2a=144√2 /2×12√2=144√2/24√2=144/24=6см
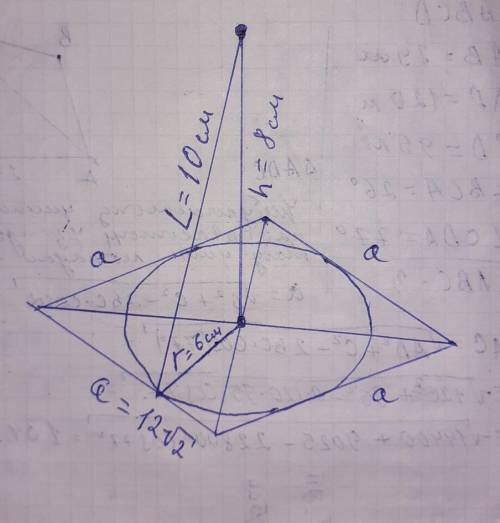
точка находится перпендикулярно к оси пересечения диагоналей ромба, и образует прямоугольный треугольник относительно к оси пересечения диагоналей и одной стороны ромба. где расстояние от точки до стороны ромба является гипотенузой, а радиус вписанной окружности катетом . а неизвестное расстояние от точки до плоскости ромба высотой и вторым катетом.
по теореме Пифагора a²+b²=c²
катет a=r=6см радиус вписанной окружности в ромб,
гипотенуза с=L=10см расстояние от точки до стороны ромба ,
катет b=h высота, расстояние от точки до плоскости ромба ,
находим h=√(L²-r²)=√(10²-6²)=√(100-36)=√64=8см
1)Так как трапеция АВСD - равнобедренная, то DP = AH = 2,8 см, поэтому HP=HD-DP=6,8 см - 2,8 см = 4 см;
AD=AH+HD=2,8см + 6,8см= 9,6см.
2) Четырёхугольник HBCP - прямоугольник, поэтому BC = HP = 4 см.
3) Угол HBC = 90 градусов, а так как угол АВС = 135 градусов, то угол АВН=угол АВС- угол НВС = 45 градусов. Треугольник АВН - прямоугольный (угол Н =90 градусов, угол В=45 градусов) и равнобедренный, поэтому ВН=АН=2,8 см.
4)Площадь АВСD = (AD+BC)/2*BH=6,8см * 2,8 см =19,04см^2
ответ: 19,04 см^2
Объяснение:
Изи)
СН-высота
уголНСВ=90-56=34°
уголСЕВ=90/2=45°(биссектриса)
=>уголЕСН=45-34=11°
ответ:11°
(прости за рисунок, но лучше нарисовать не смогу)