ответ: 864√3 см³
Объяснение:
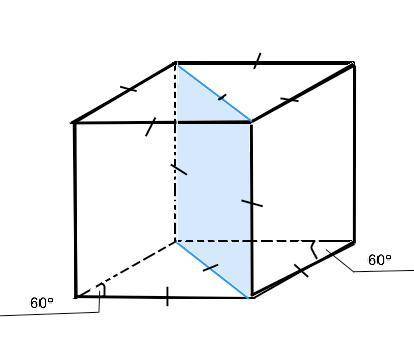
Так как основание призмы ромб с острым углом 60°, меньшая диагональ делит его на два равносторонних треугольника с равными углами при их основании ( меньшей диагонали). Поэтому высота призмы равна этой диагонали как сторона квадратного сечения, т.е. h=12 см. Объём призмы находят произведением площади основания на высоту ромба.
V=S•h.
Площадь параллелограмма равна произведению соседних сторон на синус угла между ними. Ромб - параллелограмм с равными сторонами. S=a²•sin60°=12²•√3/2=72√3 см² ⇒
V=72√3•12=864√3 см³
1) трикутники BАN і ВСА подібгні за двома кутами
<BAN=<BCA - за умовою
<NBA=<ABC=<B - очевидно (один і той самий кут)
2) середня лінія трикутника паралельна відповідній стороні трикутника, а її довжина дорівнює половині цієї сторони
NK=1/2*AC
трикутники NBK і АВС подібні з коефіцієнтом подібності k=NK/AC=1/2=0.5
(трикутник АВC подібний трикутнику NBK з коефіцієнтом подібності k*=AC/NK=2)
відповідь: 0.5
трикутники NBK і АВС подібні за двома кутами
кут NBK=кут ABC - очевидно (один і той самий кут)
кут BNK=кут ВАС - як відповідні при паралельних прямих NK||AC і січній AB
5/25=1/5 к. подобия
наименьшая сторона в 1 - 3
3*5=15