Объяснение:
Разделим тождество на две части и решим каждого:
1+ tg×(180°- a)×sin×(90°-a)×sin a = cos²×(180°- a)
1) 1+ tg×(180°- a)×sin×(90°-a)×sin a
Сначало по формулам приведения переведем тригоном. функции:
1-tg a × cos a × sin a
Дальше,раскрываем тангенс по формуле: tg a =sin a/cos a :
1-sin a/cos a × cos a × sin a
Сокращаем cos a и получаем:
1-sin² a=> по осн. тригоном. тожд. => cos² a
2)cos²×(180°- a)
Воспользуемся формулой приведения:
cos²×(180°- a)= - cos²a
По основ. тригоном.тождеству sin²a+cos²a=1 =>cos²a=1-sin²a :
- cos²a = -(1-sin²a) = -1+sin²a=sin²a-1=cos²a
В первой части тождества получили: cos² a
И во второй части получили: cos² a
Поэтому:
cos² a=cos² a
Ч.т.д
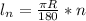, где n - градусная мера соответственного центрального угла.
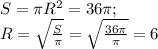, где S - площадь круга.
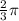см.
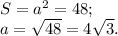
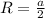, где a - сторона квадрата.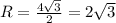
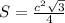, где c - сторона правильного треугольника.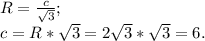
.
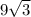см.
