Найдем гипотенузу АВ по теореме Пифагора:
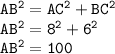
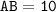 см.
см.
Свойства пропорциональных отрезков прямоугольного треугольника
1. Каждый катет есть пропорциональное между гипотенузой и проекцией катета на гипотенузу, то есть
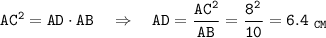
Тогда отрезок BD равен:  см.
см.
2. Высота, опущенная из вершины прямого угла на гипотенузу есть среднее пропорциональное между проекциями катетов, то есть:
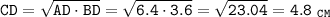
ответ: 4,8 см.
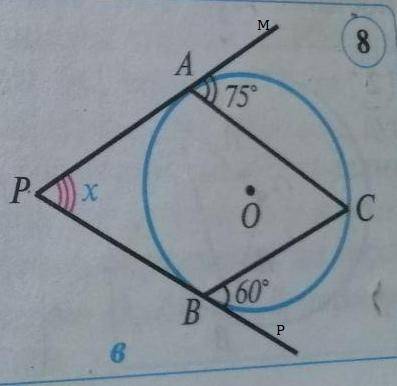
Объяснение:
ОА⊥DА по свойству касательной , ∠DАО=90°.
∠х+∠ВАО=90° и ∠х=∠ВАО=45°
ΔВАО-равнобедренный, т.к. ОВ=ОА , поэтому углы при основании равны ∠В=∠ВАО=45°, тогда центральный угол ∠ВОА=180°-2*45°=90°⇒ дуга ∪АВ=90°.
"Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами"⇒∠х=90°:2=45°
2) "Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами"⇒ ∠Р=(∪АВ-∪АС):2
25°=(80°-х):2
50°=80°-х
х=30°
3)∠МАС=75°, ∠РВС=60° . По правилу об угле, образованном касательной и хордой, проходящей через точку касания ⇒∪АС=150° и ∪ВС=120°. Значит на ∪АВ остается ∪АВ=360°-150°-120°=90°.
∠С-вписанный и опирается на ∪АВ⇒∠С=45°.
ДАЛЬШЕ МОЖНО ТАК.......По т. о смежных углах ∠РАС=180°-75°=105° и ∠РВС=180°-60°=120°
Сумма углов четырехугольника 360° , х=360°-105°-45°-120°=90°
ИЛИ МОЖНО ТАК..........Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами⇒ х= ((120°+150°)-90° ):2=90°
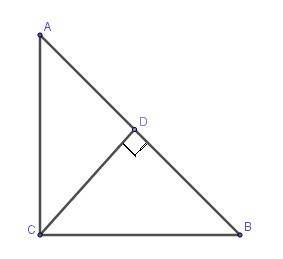
По теореме Пифагора:
АВ² = ВС² + АС²
АВ² = 8² + 6² = 64 + 36 = 100
Значит, АВ = 10 см
2) Площадь прямоугольного треугольника рассчитывается по формуле через катеты:
S = 1/2 × a × b = 1/2 × BC × AC = 1/2 × 6 × 8 = 24 см²
Но с другой стороны площадь треугольника вычисляется по стороне и высоте, проведенной к этой стороне →
S = 1/2 × AB × CD
24 = 1/2 × 10 × CD
24 = 5 × CD
Значит, CD = 24/5 = 4,8 см
ОТВЕТ: 4,8 см