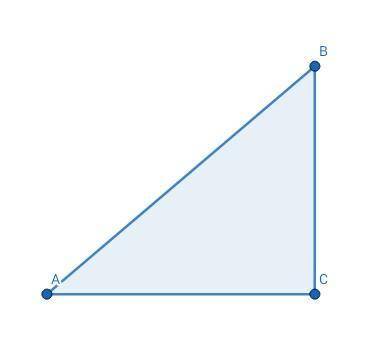
1 случай, где катет ВС = 4,2 см
Если катет равен половине гипотенузы, то напротив лежащий угол равен 30°.
=> ∠А = 30°.
Сумма острых углов прямоугольного треугольника равна 90°.
∠В = 90° - 30° = 60°
ответ: 60°, 30°.
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
2 случай, где АС = 4,2 см.
Если катет равен половине гипотенузы, то напротив лежащий угол равен 30°.
=> ∠В = 30°
Сумма острых углов прямоугольного треугольника равна 90°.
∠А = 90° - 30° = 60°
ответ: 30°, 60°.
ответ:см объяснение
Объяснение:
1) Напротив самой большой стороны лежит самый большой угол. Самая большая сторона - это АС. Она лежит напротив ∠В. Значит ∠В - наибольший. АВ - наименьшая сторона. Лежит напротив ∠С. Значит ∠С - наименьший.
2)-
3)Да,существует,так как сумма двух сторон не превышает размер третьей
4) Угол а=180-120=60°
Угол С=90-60=30°
Катет лежащий против угла 30° равен половине гипотенузы. АС=7,5*2=15
5)-
6) угол А=70, значит угол В=180-70-90=20
CD - биссектрисса,значит она делит угол С пополам.
Угол BCD равен 45 . угол BDC= 180-45-20=115
ABCD основание, ВD-меньшая диагональ,так как угол А=60 гр., то треуг. ABD равностороннний и BD=6. BB1 высота.УголB1DB=45, тогда треуг.B1BD рвнобедр.(два равных угла) и B1B=6
S=Sбок.+2Sоснов.
Sбок.=Pоснов.*BB1=24*6=144
Sоснов.=6*6*sin 60=18*корень из 3
S=144+36*корень из 3