Теорема синусов гласит, что стороны треугольника пропорциональны синусам противолежащих углов, то есть:
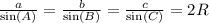
В нашем случае a=BC, b=AC, c=AB, а R — радиус описанной окружности.
4.
BC=6√3, AB=6√2, ∠A=60°
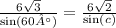
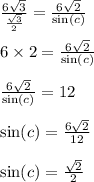
Угол C может быть 45° или 135° (по таблице синусов), но так как у треугольника сумма внутренних углов 180°, а 135°+60°=195°, что уже больше 180°, поэтому угол С равен 45°. А еще по условию треугольник остроугольный, а 135° — тупой угол.
5.
BC=4√3, A=60°. R-?
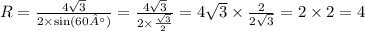
Радиус описанной окружности 4.
6.
R=14, A=30°, BC-?
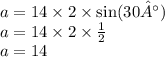
BC=14
и соответствующие углы равны A=A1 ,B=B1, C=C1
Признаки равенства:
Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Второй признак равенства треугольников. Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
Третий признак равенства треугольников. Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.