
1.наибольший угол лежит ПРОТИВ наибольшей стороны АС=10см, и это угол В=90°, просто треугольник избитый, египетский.)
2. Значит, второй равен 60°, т.к. сумма острых угло в прямоугольном треугольнике равна 90°.
3. Значит третий равен 180°-100°=80°, т.к. сумма всех углов в треугольнике равна 180°.
4. Еще как существует!) он является прямоугольным, т.к. 3²+4²=5²
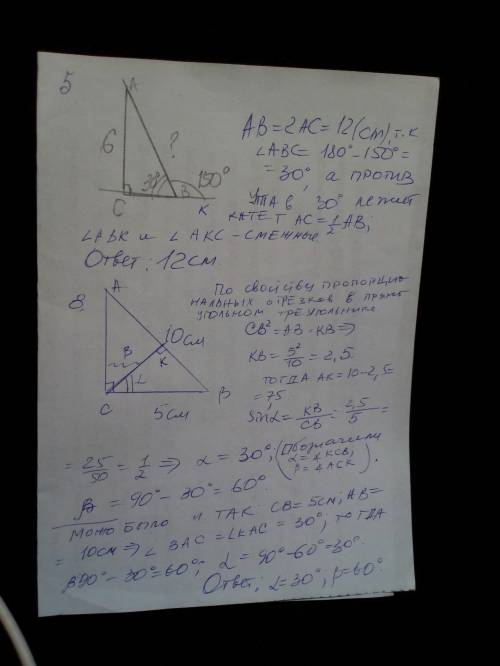
5. во вложении
6. пусть х- коэффициент пропорциональности, тогда 3х+х+2х=180, х=30, меньший угол 30°, второй угол 2*30°=60°, и третий 3 *30°=90°
8. во вложении
1)сумма углов = 360
(угол 1 + угол 2) = (угол 3 + угол 4)=360/2=180
по условию усли (угол 1)=х, то (угол 2)=3*х.
Следовательно: х+3*х=180; х=4 - углы 1 и 3; 3*45=135 - углы 2 и 4.
2)Периметр=2*(a+b).
По условию если сторона1=х, то сторона2=х+4.
следовательно: 2*(х+х+4)=36; 2х=18; х=7 - сторона1 и сторона3; 7+4=11 - сторона2 и сторона4.
3)Т.к. в параллелограмме угол1=30, то противоположный ему угол3=30. а угол2=угол4=(360-2*30)/2=150.
проведем из угла б перпендикуляр BH к СD, угол CBD=180-30-90=60. Напротив угла в 30 градусов лежит катет равный половине гипотенузы.
Следовательно сторона BC=8*2=16 и сторона AD=16.
Т.к. Периметр=2*(a+b)=52, то a+b=26. Следовательно стороны AB=СD=26-16=10.
S =S(ABC) -?
S(ADC) =S(AEC) ⇔AC*h₁/2 =AC*h₂/2 ⇒h₁ =h₂ следовательно
DE || AC ,т.е. четырехугольник ADEC есть трапеция.
ΔAOC ~ΔDOE⇒(AC/DE)² =S(AOC) /S(DOE) ⇒(AC/DE)²=4.
S(ADEC) =( √S(DOE)+√S(AOC) )² =(√2 +√8)²=(√2 +2√2)² =(3√2)²=18.
---
ΔABC~~DBC .
S(ABC)/S(DBC) =(AC/DE)² .
S/ (S - S(ADEC)) =(AC/DE)² ;
S/(S -18) =4 ⇔S =4S -72⇔S =24.
ответ: 24.
* * * P.S. S(AOC)*S(DOE)=S(AOD)*S(COE) ;
S(AOD) =S(ADC) -S(AOC) =S(AEC) -S(AOC) =S(COE)