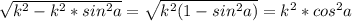Много площадь треугольника авс равна 1. на сторонах ав, вс, са, взяты соответственно точки а1, в1, с1 так, что аа1 : а1в = 1: 2, вв1 : в1с = 1: 3, точка с1 делит сторону ас пополам. найдите площадь треугольника а1в1с1.

👇

Ответ:

lapysh1995

25.12.2021

Есть теорема: Площади треугольников, имеющих равный угол, относятся как произведения сторон, содержащих этот угол. В нашем случае:

Sa1bb1/Sabc = A1B*BB1 = (2/3)AB*(1/4)*BC/AB*BC.

Таким образом, Sa1bb1 = 1/4 (так как Sabc=1 - дано).

Аналогично, Saa1c1/ABC = (1/3)AB*(1/2)АС/АВ*АС.

То есть Saa1c1=1/6.

Scc1b1/ABC = (1/2)AC*(3/4)BC/АC*BС.

То есть Scc1b1=3/8.

Sa1b1c1 = Sabc - Sa1bb1 - Saa1c1 - Scc1b1.

Sa1b1c1 = 1 - 1/4 - 1/6 - 3/8 = 1 - 19/24 = 5/24.

ответ: Sa1b1c1 = 5/24.

Много площадь треугольника авс равна 1. на сторонах ав, вс, са, взяты соответственно точки а1, в1, с

4,6(72 оценок)

Открыть все ответы

Ответ:

vanyalebedev1248

25.12.2021

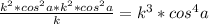
3) найдем СВ....используем теорему синусов...к/sin 90=СВ/sina....отсюда: (синус 90 градусов равен 1)...СВ=к*sina...далее, по следствию из т. Пифагора найдем АС: $\sqrt{ k^{2}- k^{2}* sin^{2}a } = \sqrt{ k^{2}(1- sin^{2}a) } = k^{2} * cos^{2}a$ ... теперь находим АД, используя подобие треугольников.... $\frac{ k^{2}* cos^{2} }{k}= \frac{AD}{k^{2}* cos^{2} }$ .... значит, АД= $\frac{ k^{2}* cos^{2}a*k^{2}* cos^{2}a }{k}= k^{3} * cos^{4}a$

4) в параллелограмме высоты будут равные....найдем одну из них, используя метод площадей...т.е. S=a*h....S=a*b*sina...(a и b - стороны....синус альфа - синус углы между этими сторонами....h - высота)...прировняв два метода нахождения площади, получим, что h=2 корень из 2

1) сторону АС найдем через определение тангенса угла альфа...т.е. tga=CB/AC...AC=CB/tga=5/tga

2) используем основное тождество, чтобы найти косинус (через него найдем тангенс)... $cos^{2}a=1- sin^{2}a$
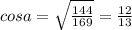
$cosa= \sqrt{ \frac{144}{169} } = \frac{12}{13}$
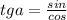
$tga= \frac{sin}{cos}$
tg=5/13 * 13/12=5/12

4,4(31 оценок)

Ответ:

bestgad

25.12.2021

3√3/2 см.

Объяснение:

Если тригонометрические соотношения в прямоугольном треугольнике ещё не изучены, можно воспользоваться этим

1. Центром окружности, описанной около прямоугольного треугольника, является середина гипотенузы, тогда длина гипотенузы с = 2R = 2•3 = 6(см).

2. По условию один из острых углов треугольника равен 60°, тогда второй острый угол равен 90° - 60° = 30°. Напротив него лежит катет, равный половине гипотенузы, а = 6:2= 3 (см).

3. По теореме длина второго катета b = √(36 - 9) = √27 = 3√3(см).

4. S = 1/2ab,

S = 1/2• c • h, тогда

1/2•a•b = 1/2• c • h,

ab = ch,

h = (ab)/c = (3•3√3)/6 = 3√3/2 (см).

4,5(44 оценок)

Это интересно:

Кулинария-и-гостеприимство

13.05.2023

Как отчистить старые кастрюли быстро и безопасно...

Праздники-и-традиции