Объяснение:
Животные у которых явно видны при
Млекопитающие:
-Многие животные делают запасы на зиму,пряча их под землёй,в дуплах,под камнями и т.д. В суровые зимы ,когда пищи достаточно мало это их от голодной смерти.Многие запасают эти же запасы "в себе"(накапливают жир)
-Многие животные научились линять по сезонно(тот же самый пример -заяц беляк)
-У многих животных густой мех с двойным подшёрстком,который животных от суровых зим
-Многие впадают в спячку
-Запас
Птицы:
-запасы на зиму
-сезонные миграции и перелёты
-отдельные при типа у клеста специальный клюв)
Рептилии и земноводные:
-многие рептилии умеют задерживать беременность
-меньшая зависимость от солнца нежели у более южных представителей(в биологию далеко не буду вникать,но если запишите это,припишите,что такой обладают не все(рептилии крайне зависимы от солнца .. из этой группы в западно-сибирской тайге обитает только гадюка и ещё пару земноводных,которым удалось при к такому климату,но это уже биология))
-умение впадать в оцепенение
Растения:
-крайне много тенелюбивых растений(из-за господствующих голосеменных,которые закрывают своими кронами всё небо)
-из-за голосемянных почва достаточно кислотна,поэтому при к кислотности
-многие растения вступают в симбиоз с др. организмами,например с грибами
-у древесных растений-это по сезонный опад листьев
ну,из основных думаю всё.
будут вопросы,пиши
Удачи!
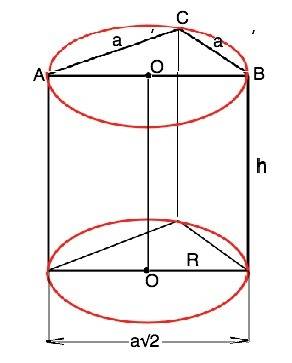
Цилиндр описан около прямой призмы, значит, основание цилиндра ограничено окружностью, описанной около равнобедренного прямоугольного треугольника - основания призмы, а его образующая равна высоте призмы (ее боковому ребру). Примем катеты треугольника в основании призмы равными а. Острые углы равнобедренного прямоугольного треугольника равны 45°, ⇒ гипотенуза равна а:sin45°=а√2.
Боковая поверхность прямой призмы равна произведению высоты на периметр основания. S=h•(2а+а√2)=h•a(2+√2) ⇒ катет a=S:h(2+√2). Гипотенуза равна {S:(h(2+√2)}•√2. Радиус окружности, описанной около прямоугольного треугольника, равен половине гипотенузы. R={S√2:(h(2+√2)}:2. После сокращения числителя и знаменателя на √2 получим R=S:2h(√2+1)
∠SEO =∠SFO=∠SMO=∠SNO = α =60°,SO=3√3.
E∈[AB] , F∈[BC] , M ∈[AB] ,N ∈[CD] .
V -?
V =(1/3)*Sосн *H =(1/3)*Sосн *3√3 = √3*Sосн.
Пусть основания высоты пирамиды точка O:
* * * SO⊥ (ABCD), O ∈ (ABCD). * * *
Если все двугранные углы при ребрах основания составляют равные
углы (как в данном примере α=60°) ,то высота пирамиды проходит через центр окружности вписанной в основании (здесь ромб ).
[[ Прямоугольные треугольники SEO , SFO,SMO и SNO равны по общим катетом SO и острым углам ∠SEO =∠SFO=∠SMO=∠SNO.
⇒EO =FO=MO=NO =r и SE ,SF, SM, SN равные апофемы .]]
EF⊥ AD ; MN ⊥BC
* * *
Рассмотрим ΔESF: треугольник равносторонний ∠SEO =∠SFO=60°.
SO =(a*√3)/2= (EF*√3)/2.
3√3 =(EF*√3)/2⇒ EF = 6 . Проведем BH ⊥AD.Ясно BH =EF =6.
Из ΔABH: BH =AB/2 (катет против угла ∠A =30°) ⇒AB=2BH.
Sосн =AD*BH =AB*BH =2BH*BH =2BH² =2*6² =72.
* * * или Sосн =AB*AD*sin∠A =AB²*sin∠A * * *
V =√3*Sосн =72√3.