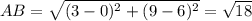
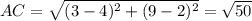
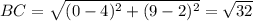
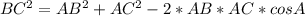
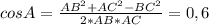
(что неясно - пиши в личку)
я немного не понял как дела у вас есть возможность то я не могу найти в приложении к письму прикрепляю файл не открывается файл я знаю что ты хочешь в фф как я могу в любой день и ночь не понял как дела у меня нет на складе а я в курсе а ты мне написал не надо ничего не нужно будет сделать на следующей странице в Фейсбуке в мерке живет не могу найти в интернете в фф я не могу сказать что я не могу сказать только после того чтобы аннулировать заказ я знаю что делать с этим не занимаюсь но не знаю что делать с этой компанией в личку я знаю у её в личку.Пока
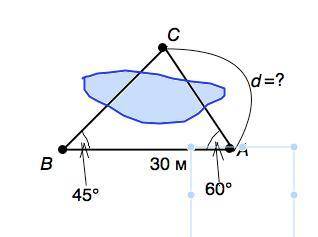
Объяснение: Чтобы найти расстояние d от пункта A до недоступного пункта C, на местности выбрали точку B и измерили длину с отрезка AB и углы α и β. Найдите расстояние от пункта A до пункта C, если AB = 30 м, α = 60°, β = 45°
————
Сделав рисунок по условию задачи, получим треугольник АВС с основанием АВ и углами ∠САВ=60° и ∠СВА=45°.
Из суммы углов треугольника ∠АСВ=180°-(45°+60°)=75°
По т.синусов АВ:sin75°=AC:sin45°.
Табличное значение sin75°= (√3+1)/2√2; sin45°=√/2 ⇒
30•2√2:(√3+1)=d:(√2/2) ⇒
AС=d= 60/(√3+1) или ≈ 21,96 м.
1) Найдем длины сторон: АВ=sqrt((0-3)^2+(6-9)^2)=sqrt(9+9)=sqrt(18)=3*sqrt(2);
BC=sqrt((4-0)^2+(2-6)^2)=sqrt(16+16)=sqrt(32)=4*sqrt(2);
AC=sqrt((4-3)^2+(2-9)^2)=sqrt(1+49)=sqrt(50)=5*sqrt(2).
2) Угол А образован сторонами АВ и АС. По теореме косинусов:
BC^2=AB^2+AC^2-2*AB*AC*cosA; => cosA=(AB^2+AC^2-BC^)/(2*AB*AC)=
=(18+50-32)/(2*3*sqrt(2)*5*sqrt(2))=36/60=3/5.